��Ŀ����
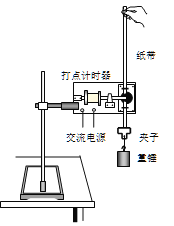
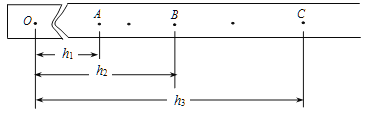
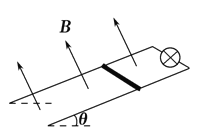
����Ŀ����ͼ��ʾ�������㹻�������費�������L��0��2 m��ƽ�н�������̶�����Ǧȣ�37��ľ�Եб���ϣ����˽���һ�����ѹU��4 V��С���ݣ����������һ�Ÿ�Ӧǿ�ȴ�СB��5 T������ֱб�����ϵ���ǿ�ų�����һ����Ϊ2L������m��0��2 kg������r��1��0 ���Ľ�������ֱ�ڵ�������ڶ��˸������ٶ��ͷţ��������뵼��Ӵ����ã��������뵼���Ķ�Ħ�������̣�0��25����֪�������»����ٶ��ȶ�ʱ��С����ǡ���������⣬�������ٶ�gȡ10 m/s2��sin 37�㣽0��6��cos 37�㣽0��8����
��1���������տ�ʼ�˶�ʱ�ļ��ٶȴ�С��
��2���������ȶ��»�ʱ���ٶȴ�С��
���𰸡���1��4 m/s2����2��4��8 m/s
�������������������1���������տ�ʼ�˶�ʱ���ٶ�Ϊ�㣬���ܰ��������ã���ţ�ٵڶ����ɵã�
mgsin ������mgcos ����ma���������ݵã�a��4 m/s2��
��2����������ȶ��»�ʱ���ٶ�Ϊv����Ӧ�綯��ΪE������������Ч����ΪL������·�еĵ���ΪI����ƽ�������ã�mgsin ����BIL����mgcos �� ��
�ɱպϵ�·ŷķ���ɵ�![]() ��
��
�ɷ����ڵ�Ÿ�Ӧ���ɵ�E��BLv ��
�����٢ڢ���ã�v��4��8 m/s��

 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�