��Ŀ����
��ͼ��ʾ����X��0��Y��0�Ŀռ��д���������ˮƽ��MNΪ�磬�Ÿ�Ӧǿ�ȴ�С��ΪB�������෴����ǿ�ų���һ���϶˿��ڡ��ڱڹ⻬�ľ�Եϸ�ܣ���ΪL����ײ���һ����Ϊm������Ϊ+q�����ӣ���ˮƽ���������£�����ϸ��ʼ��ƽ����Y�ᣬ��X�������ٶ�v0���������˶�����B=
���������ӵ���������
��1��ϸ�ܸս���ų�ʱ�������˶��ļ��ٶȴ�С������
��2��ά��ϸ��ʼ��ƽ����Y�����������˶��Ĺ����У�ˮƽ���������Ĺ���
��3�����ӵ�һ�ε����˶��켣��ߵ��λ�����꣮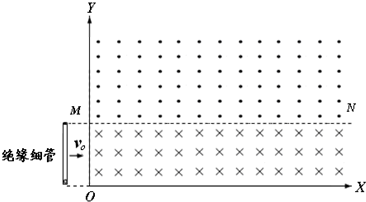
| mv0 |
| 2qL |
��1��ϸ�ܸս���ų�ʱ�������˶��ļ��ٶȴ�С������
��2��ά��ϸ��ʼ��ƽ����Y�����������˶��Ĺ����У�ˮƽ���������Ĺ���
��3�����ӵ�һ�ε����˶��켣��ߵ��λ�����꣮

��1��������Ϊ�о��������Ӹս���ų�f1=qv0B a1=
=
��+Y����
��2�������뿪������ǰ���ڹ�����ֱ�������ȼ���ֱ���˶���ˮƽ�����������˶����������ڹ�����ֱ�����������˶��ļ��ٶ�a�������˶����ܿ�ʱ����������ֱ����ķ���Ϊv1����
����ֱ���� a=a1 v12=2aL
�ɽ�� v1=v0
�����뿪�����ܿ�ʱ���ٶ� v��=
=
v0m/s
�ٶȷ�����MN��45���
������������
�й��ܹ�ϵ WF=��Ek ��EK=
m
�ɵ� WF=
m
��3�������뿪�ܿں��ڴų���������Բ���˶�
�ڴų��� qv��B=m
r=
=2
L
�����ڹ����˶���ʱ��t =
=
�����ڹ����˶��Ĺ����з�����ˮƽλ�ơ�x=v0t=2L
�켣��ߵ��λ�����꣺x=��x+r?sin45��=4L y=L+r(1-cos450)=(2
-1)L����
| qv0B |
| m |
| v02 |
| 2L |
��2�������뿪������ǰ���ڹ�����ֱ�������ȼ���ֱ���˶���ˮƽ�����������˶����������ڹ�����ֱ�����������˶��ļ��ٶ�a�������˶����ܿ�ʱ����������ֱ����ķ���Ϊv1����
����ֱ���� a=a1 v12=2aL
�ɽ�� v1=v0
�����뿪�����ܿ�ʱ���ٶ� v��=
v2+
|
| 2 |
�ٶȷ�����MN��45���
������������
�й��ܹ�ϵ WF=��Ek ��EK=
| 1 |
| 2 |
| v | 20 |
�ɵ� WF=
| 1 |
| 2 |
| v | 20 |
��3�������뿪�ܿں��ڴų���������Բ���˶�
�ڴų��� qv��B=m
| v��2 |
| r |
| mv�� |
| qB |
| 2 |
�����ڹ����˶���ʱ��t =
| L | ||
|
| 2L |
| v0 |
�����ڹ����˶��Ĺ����з�����ˮƽλ�ơ�x=v0t=2L
�켣��ߵ��λ�����꣺x=��x+r?sin45��=4L y=L+r(1-cos450)=(2
| 2 |

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
 ��ͼ��ʾ����x��0��y��0���ڢ����ޣ��Ŀռ������y�Ḻ�������ǿ�糡����ǿ��СΪE��һ������Դ������ͬ�Ĵ��������ӣ����ӵij��ٶȺ㶨������y���ϵ�P��0��2L������x��������������ǿ�糡�У����Ӿ��糡���ú�ǡ�ô�x���ϵ�Q��L��0�������������ȥ�糡���ڴ������һ����ֱ��xoyƽ�����ǿ�ų����Ÿ�ǿ�ȴ�СΪB�������������䣬������ǡ�ô�Q������������ӵ�����������֮�������ã���ȡ��
��ͼ��ʾ����x��0��y��0���ڢ����ޣ��Ŀռ������y�Ḻ�������ǿ�糡����ǿ��СΪE��һ������Դ������ͬ�Ĵ��������ӣ����ӵij��ٶȺ㶨������y���ϵ�P��0��2L������x��������������ǿ�糡�У����Ӿ��糡���ú�ǡ�ô�x���ϵ�Q��L��0�������������ȥ�糡���ڴ������һ����ֱ��xoyƽ�����ǿ�ų����Ÿ�ǿ�ȴ�СΪB�������������䣬������ǡ�ô�Q������������ӵ�����������֮�������ã���ȡ�� ��ͼ��ʾ����x��0��y��0�Ŀռ�����һ��ǿ�ų����Ÿ�Ӧǿ�ȵķ���ֱ��xOyƽ�������СΪB������һ����Ϊm������Ϊq�Ĵ��������ӣ�����x���ϵ�ij��P������x���30��ǵķ�������ų�������������Ӱ�죬�������й�˵������ȷ���ǣ�������
��ͼ��ʾ����x��0��y��0�Ŀռ�����һ��ǿ�ų����Ÿ�Ӧǿ�ȵķ���ֱ��xOyƽ�������СΪB������һ����Ϊm������Ϊq�Ĵ��������ӣ�����x���ϵ�ij��P������x���30��ǵķ�������ų�������������Ӱ�죬�������й�˵������ȷ���ǣ������� ��ͼ��ʾ����x��0��y��0�Ŀռ����к㶨����ǿ�ų����Ÿ�Ӧǿ�ȵķ���ֱ��xOyƽ�������СΪB������һ����Ϊm������Ϊq�Ĵ������ӣ���x���ϵ�ԭ��ľ���Ϊx0��P�㣬��ƽ����y��ij��ٶ�����ų����ڴų��������ش�ֱ��y��ķ�������ų�������������Ӱ�죬����Щ��Ϣ����ȷ�����ǣ�������
��ͼ��ʾ����x��0��y��0�Ŀռ����к㶨����ǿ�ų����Ÿ�Ӧǿ�ȵķ���ֱ��xOyƽ�������СΪB������һ����Ϊm������Ϊq�Ĵ������ӣ���x���ϵ�ԭ��ľ���Ϊx0��P�㣬��ƽ����y��ij��ٶ�����ų����ڴų��������ش�ֱ��y��ķ�������ų�������������Ӱ�죬����Щ��Ϣ����ȷ�����ǣ������� ��ͼ��ʾ����x��0��y��0�������ڴ��ڴ�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB����x��0��y��0�������ڴ�����y�����������ǿ�糡��һ����Ϊm�������Ϊq�Ĵ������Ӵ�x���ϵ�M����y�Ḻ����ֱ����ų�������������Ӵ�y���N������ų���������ǿ�糡�����糡ƫת���x���ϵ�P�㣬��֪
��ͼ��ʾ����x��0��y��0�������ڴ��ڴ�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB����x��0��y��0�������ڴ�����y�����������ǿ�糡��һ����Ϊm�������Ϊq�Ĵ������Ӵ�x���ϵ�M����y�Ḻ����ֱ����ų�������������Ӵ�y���N������ų���������ǿ�糡�����糡ƫת���x���ϵ�P�㣬��֪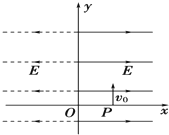 ��ͼ��ʾ����x��0�Ŀռ��ڴ�����x�����������ǿ�糡���糡ǿ��ΪE����x��0�Ŀռ��ڴ�����x�Ḻ�������ǿ�糡����ǿ��СҲ����E��һ���ӣ�-e��m����x=d����P������y��������ij��ٶ�v0��ʼ�˶������Ƶ�����������
��ͼ��ʾ����x��0�Ŀռ��ڴ�����x�����������ǿ�糡���糡ǿ��ΪE����x��0�Ŀռ��ڴ�����x�Ḻ�������ǿ�糡����ǿ��СҲ����E��һ���ӣ�-e��m����x=d����P������y��������ij��ٶ�v0��ʼ�˶������Ƶ�����������