��Ŀ����
��ͼ��ʾ���������ΪL�Ľ�������̶���ˮƽ���ϣ�������費�ƣ�һ������Ϊm����ΪL������ΪR�Ľ��������˷��ڵ����ϣ��������������Ķ�Ħ������Ϊ?�����뵼��ĽӴ����費�ƣ��������������ֵΪ2R�ĵ��裮 ��n����ֱ���¿���Ϊa����ǿ�ų����ҴŸ�Ӧǿ��ΪB�����ڴų����ļ��Ϊb��a��b������������ʼλ��OO�䴦�����һ�δų����2a��������������Ϊ�㣬�ֶ�ʩ��ˮƽ���ҵĺ㶨����F��ʹ���������δų������ֽ�������������Ϊb�ķǴų������ʱ����ͬ��
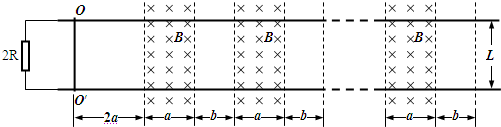
��1�������������һ�δų�ʱ���ٶȺʹ�ʱ�ų��Խ���������������
��2���ڽ������ӽ����һ�δų����ӵ�n�δų������Ĺ����У�������˵����ϲ�����������

��1�������������һ�δų�ʱ���ٶȺʹ�ʱ�ų��Խ���������������
��2���ڽ������ӽ����һ�δų����ӵ�n�δų������Ĺ����У�������˵����ϲ�����������
��������1�������������һ�δų�ǰ�ܵ������ͻ���Ħ�������ã����ݶ��ܶ����������������һ�δų�ʱ���ٶȣ���E=BLv��I=
��F=IBL����������Ĵ�С�������ֶ����жϰ������ķ���
��2�������⣬��������������Ϊb�ķǴų������ʱ����ͬ�����ٶ�Ҳ��ͬ��������ų�ʱ���ٶȾ���ͬ�����ڽ����������һ�δų�ʱ���ٶ�v1���뿪���ų�ʱ���ٶ�Ҳ��ͬ��Ӧ���ڽ������뿪��һ�δų�ʱ���ٶ�v2�����ݶ��ܶ����ֱ��о������������Ǵų�������̣��õ��ٶ�v2���ɶ��ܶ����������������ÿ�δų������ĵ��ܣ����ɴ�����·�ص����������˵����ϲ�����������
| E |
| R+r |
��2�������⣬��������������Ϊb�ķǴų������ʱ����ͬ�����ٶ�Ҳ��ͬ��������ų�ʱ���ٶȾ���ͬ�����ڽ����������һ�δų�ʱ���ٶ�v1���뿪���ų�ʱ���ٶ�Ҳ��ͬ��Ӧ���ڽ������뿪��һ�δų�ʱ���ٶ�v2�����ݶ��ܶ����ֱ��о������������Ǵų�������̣��õ��ٶ�v2���ɶ��ܶ����������������ÿ�δų������ĵ��ܣ����ɴ�����·�ص����������˵����ϲ�����������
����⣺��1�������������һ�δų�ǰֻ�ܺ㶨����F��Ħ��������
��(F-��mg)��2a=
mv12
v1=
E=BLv1
I=
=
�ã�F��=IBL=
������
��2�����ڽ���������������Ϊb�ķǴų������ʱ����ͬ�Ҽ��ٶ�Ҳ��ͬ��˵����������ų�ʱ���ٶȾ���ͬ�����ڽ����������һ�δų�ʱ���ٶ�v1���뿪���ų�ʱ���ٶ�Ҳ��ͬ��Ӧ���ڽ������뿪��һ�δų�ʱ���ٶ�v2��
�����Ǵų�������̣�(F-��mg)b=
m
-
m
��� v2=
ÿ����һ�δų������ĵ�����ͬ����ΪE�������ݶ��ܶ�������
Fa-��mga-E��=
mv22-
mv12
���ԣ�
Q=
��2R=
n(F-��mg)(a+b)
��
��1�������������һ�δų�ʱ���ٶ�Ϊ
����ʱ�ų��Խ�������������Ϊ
��
��2���ڽ������ӽ����һ�δų����ӵ�n�δų������Ĺ����У�������˵����ϲ���������Ϊ
n(F-��mg)(a+b)��
��(F-��mg)��2a=
| 1 |
| 2 |
v1=
|
E=BLv1
I=
| E |
| 3R |
| BLv1 |
| 3R |
�ã�F��=IBL=
| B2L2 |
| 3R |
|
��2�����ڽ���������������Ϊb�ķǴų������ʱ����ͬ�Ҽ��ٶ�Ҳ��ͬ��˵����������ų�ʱ���ٶȾ���ͬ�����ڽ����������һ�δų�ʱ���ٶ�v1���뿪���ų�ʱ���ٶ�Ҳ��ͬ��Ӧ���ڽ������뿪��һ�δų�ʱ���ٶ�v2��
�����Ǵų�������̣�(F-��mg)b=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
��� v2=
|
ÿ����һ�δų������ĵ�����ͬ����ΪE�������ݶ��ܶ�������
Fa-��mga-E��=
| 1 |
| 2 |
| 1 |
| 2 |
���ԣ�
|
Q=
| nE�� |
| 3R |
| 2 |
| 3 |
��
��1�������������һ�δų�ʱ���ٶ�Ϊ
|
| B2L2 |
| 3R |
|
��2���ڽ������ӽ����һ�δų����ӵ�n�δų������Ĺ����У�������˵����ϲ���������Ϊ
| 2 |
| 3 |
������������������ǻ������ؼ�������ת�����غ�Ƕ�����⣬����ʱҪע��ץסʹ��������ų����ٶȶ���ͬ���Լ�ͨ��ÿ�δų�ʱ��·�з���������ͬ��������

��ϰ��ϵ�д�
�����Ŀ
 ��2005?��������ͼ��ʾ���������Ϊl��ƽ��ֱ����ab��cd��b��d������һ�̶�����R���������ɺ��Բ��ƣ�MNΪ����ab��cd�ϵ�һ����ˣ���ab��ֱ�������ҲΪR������װ�ô�����ǿ�ų��У��Ÿ�Ӧǿ�ȵĴ�СΪB���ų�����ֱ�ڵ�������ƽ�棨ָ��ͼ��ֽ���ڣ����ֶ�MNʩ��ʹ���ص��췽�����ٶ�v����ͼ���������˶�����U��ʾMN���˵�ѹ�Ĵ�С��������
��2005?��������ͼ��ʾ���������Ϊl��ƽ��ֱ����ab��cd��b��d������һ�̶�����R���������ɺ��Բ��ƣ�MNΪ����ab��cd�ϵ�һ����ˣ���ab��ֱ�������ҲΪR������װ�ô�����ǿ�ų��У��Ÿ�Ӧǿ�ȵĴ�СΪB���ų�����ֱ�ڵ�������ƽ�棨ָ��ͼ��ֽ���ڣ����ֶ�MNʩ��ʹ���ص��췽�����ٶ�v����ͼ���������˶�����U��ʾMN���˵�ѹ�Ĵ�С��������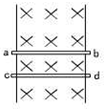 ��ͼ��ʾ���������ΪL����ֱƽ�н�������λ����ǿ�ų��У��Ÿ�Ӧǿ��ΪB��������費�ƣ���������⻬����Ӵ��Ľ�����������Ϊm�������ΪR����Ҫʹcd��ǡ��ƽ�⣬�Ҿ�ֹ��������ab��Ӧ��
��ͼ��ʾ���������ΪL����ֱƽ�н�������λ����ǿ�ų��У��Ÿ�Ӧǿ��ΪB��������費�ƣ���������⻬����Ӵ��Ľ�����������Ϊm�������ΪR����Ҫʹcd��ǡ��ƽ�⣬�Ҿ�ֹ��������ab��Ӧ��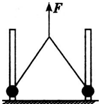 ��ͼ��ʾ���������ΪL����ֱ�̶����ϸ���������Ϊm��С��С������ڸ�����Ħ�������ɻ����������ó�Ϊ2L���������������������е�ʩ��һ����ֱ���ϵ�����F��ǡ��ʹ��������ֱ�����������˶�����ÿ��С�����ܵ�������СΪ���������ٶ�Ϊg����������
��ͼ��ʾ���������ΪL����ֱ�̶����ϸ���������Ϊm��С��С������ڸ�����Ħ�������ɻ����������ó�Ϊ2L���������������������е�ʩ��һ����ֱ���ϵ�����F��ǡ��ʹ��������ֱ�����������˶�����ÿ��С�����ܵ�������СΪ���������ٶ�Ϊg���������� ��2005?������һģ����ͼ��ʾ���������Ϊd�㹻����ƽ�й⻬��������λ��ˮƽ���xoyƽ���ڣ�һ�˽�����ֵΪR�ĵ��裮��x��0��һ�������ֱ���µ���ǿ�ų����Ÿ�Ӧǿ��ΪB��һ����Ϊr�Ľ���ֱ����������촹ֱ���ò��Ӵ����ã������˿��ڵ����ϻ�������ʼʱ������ֱ��λ��x=0������������һ��СΪv0��������x��������ij��ٶȣ����˶���������һ��С�ɵ��ڵ�����F�����ڽ������ϣ�ʹ�����˱��ִ�СΪa��������x�Ḻ����ĺ㶨���ٶ��˶����������������Բ��ƣ�
��2005?������һģ����ͼ��ʾ���������Ϊd�㹻����ƽ�й⻬��������λ��ˮƽ���xoyƽ���ڣ�һ�˽�����ֵΪR�ĵ��裮��x��0��һ�������ֱ���µ���ǿ�ų����Ÿ�Ӧǿ��ΪB��һ����Ϊr�Ľ���ֱ����������촹ֱ���ò��Ӵ����ã������˿��ڵ����ϻ�������ʼʱ������ֱ��λ��x=0������������һ��СΪv0��������x��������ij��ٶȣ����˶���������һ��С�ɵ��ڵ�����F�����ڽ������ϣ�ʹ�����˱��ִ�СΪa��������x�Ḻ����ĺ㶨���ٶ��˶����������������Բ��ƣ�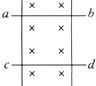 ��ͼ��ʾ���������ΪL����ֱƽ�й⻬��������λ�ڴŸ�Ӧǿ��ΪB������ֱֽ���������ǿ�ų��У�������費�ƣ������������������챣�����ýӴ��Ľ�����ab��cd������Ϊm��ab��cd����պϵ�·�ĵ����ΪR����Ҫcd��ֹ��������ʹab��ֱ��
��ͼ��ʾ���������ΪL����ֱƽ�й⻬��������λ�ڴŸ�Ӧǿ��ΪB������ֱֽ���������ǿ�ų��У�������費�ƣ������������������챣�����ýӴ��Ľ�����ab��cd������Ϊm��ab��cd����պϵ�·�ĵ����ΪR����Ҫcd��ֹ��������ʹab��ֱ��