题目内容
11. 如图所示,AB是一段半径为R的$\frac{1}{4}$圆弧曲面,在光滑水平面上一小球以某一速度运动到A点时,同停在A点的另一相同小球发生碰撞并粘在一起运动,最后落在水平地面上的C点,已知两小球没有跟圆弧曲面的任何其它点接触,则BC的最小距离为( )
如图所示,AB是一段半径为R的$\frac{1}{4}$圆弧曲面,在光滑水平面上一小球以某一速度运动到A点时,同停在A点的另一相同小球发生碰撞并粘在一起运动,最后落在水平地面上的C点,已知两小球没有跟圆弧曲面的任何其它点接触,则BC的最小距离为( )| A. | R | B. | $\frac{1}{2}$R | C. | ($\sqrt{2}$-1)R | D. | $\frac{{\sqrt{2}}}{2}$R |
分析 小球没有跟圆弧曲面的任何点接触,小球做平抛运动,根据高度求出运动的时间.由于没跟曲面接触,知在A点对接触面的压力为零,根据重力提供向心力求出平抛运动的初速度,从而得出平抛运动水平位移,即可得出BC的最小距离.
解答 解:在A点,小球开始离开圆弧曲面,只受重力,则有:$mg=m\frac{{v}^{2}}{R}$,解得v=$\sqrt{gR}$
小球做平抛运动,由R=$\frac{1}{2}g{t}^{2}$得,t=$\sqrt{\frac{2R}{g}}$,
则平抛运动的最小水平位移为:x=vt=$\sqrt{gR}\sqrt{\frac{2R}{g}}=\sqrt{2}R$
所以BC的最小距离为:d=$\sqrt{2}R-R=(\sqrt{2}-1)R$.
故选:C.
点评 本题综合运用了平抛运动和圆周运动的知识,关键掌握平抛运动的规律和圆周运动在最高点由径向的合力提供向心力.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
19. 如图所示,三根轻细绳悬挂两个质量相同的小球保持静止,A、D间细绳是水平的,现对B球施加一个水平向右的力F,将B缓缓拉到图中虚线位置,这时三根细绳张力${\;}_{{T}_{AC}}$、${\;}_{{T}_{AD}}$、${\;}_{{T}_{AB}}$的变化情况是( )
如图所示,三根轻细绳悬挂两个质量相同的小球保持静止,A、D间细绳是水平的,现对B球施加一个水平向右的力F,将B缓缓拉到图中虚线位置,这时三根细绳张力${\;}_{{T}_{AC}}$、${\;}_{{T}_{AD}}$、${\;}_{{T}_{AB}}$的变化情况是( )
 如图所示,三根轻细绳悬挂两个质量相同的小球保持静止,A、D间细绳是水平的,现对B球施加一个水平向右的力F,将B缓缓拉到图中虚线位置,这时三根细绳张力${\;}_{{T}_{AC}}$、${\;}_{{T}_{AD}}$、${\;}_{{T}_{AB}}$的变化情况是( )
如图所示,三根轻细绳悬挂两个质量相同的小球保持静止,A、D间细绳是水平的,现对B球施加一个水平向右的力F,将B缓缓拉到图中虚线位置,这时三根细绳张力${\;}_{{T}_{AC}}$、${\;}_{{T}_{AD}}$、${\;}_{{T}_{AB}}$的变化情况是( )| A. | 都变大 | B. | ${\;}_{{T}_{AD}}$和${\;}_{{T}_{AB}}$变大,${\;}_{{T}_{AC}}$不变 | ||
| C. | ${\;}_{{T}_{AC}}$和${\;}_{{T}_{AB}}$变大,${\;}_{{T}_{AD}}$不变 | D. | ${\;}_{{T}_{AC}}$和${\;}_{{T}_{AD}}$变大,${\;}_{{T}_{AB}}$不变 |
6.用轻绳系一质量为m的砝码并向上提起,当绳中张力为T=mg时,砝码匀速上升.若绳中张力变为2T,则砝码匀加速上升,其加速度a的大小为( )
| A. | a<g | B. | a=g | C. | g<a<2g | D. | a=2g |
3.下列说法中正确的是( )
| A. | 电荷所受电场力的方向就是电场强度的方向 | |
| B. | 电势降低的方向就是电场强度的方向 | |
| C. | 电场线一定与等势面垂直,并由电势高的等势面指向电势低的等势面 | |
| D. | 打雷时,呆在汽车里比呆在木屋里要危险 |
17.关于磁感应强度的单位,下列等式中哪些单位是正确的( )
| A. | 1T=1kg•A/s2 | B. | 1T=1kg/A•s2 | C. | 1T=lWb/m | D. | 1T=1N•s/C•m |

 一负电荷从电场中A点由静止释放,只受静电力作用,沿电场线运动到B点,它运动的v-t图象如图所示,则两点A、B所在区域的电场线分布情况可能是下图中的( )
一负电荷从电场中A点由静止释放,只受静电力作用,沿电场线运动到B点,它运动的v-t图象如图所示,则两点A、B所在区域的电场线分布情况可能是下图中的( )



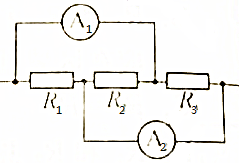 如图所示,三个电阻的阻值之比为R1:R2:R3=1:2:3,电流表的内阻忽略不计,则通过三个电阻的电流强度之比为多少?两个电流表读数之比多少?
如图所示,三个电阻的阻值之比为R1:R2:R3=1:2:3,电流表的内阻忽略不计,则通过三个电阻的电流强度之比为多少?两个电流表读数之比多少?