Question

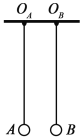
【题目】如图所示，在质量为1kg的重物上系着一条长30cm的细绳，细绳的另一端连着套在水平棒上可以滑动的圆环，环与棒间的动摩擦因数为0．75，另有一条细绳，其一端跨过定滑轮，定滑轮固定在距离圆环0．5m的地方．当细绳的端点挂上重物G，而圆环将要滑动时（环的重力忽略不计），试问：

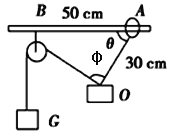
（1）角φ多大？

（2）长为30cm的细绳的张力是多少？

（3）圆环将要开始滑动时，重物G的质量是多少？

Answer 1

【答案】（1）90°（2）8N（3）0．6kg．

【解析】

试题分析：（1）因为圆环将要开始滑动，所以可以判定本题是在共点力作用下物体的平衡问题．

有：μFN－FTcosθ＝0

FN－FTsinθ＝0。

所以tanθ＝1/μ，θ＝arctan（1/μ）＝arctan（4/3）．

设想：过O作OA的垂线与杆交于B′点，由AO＝30cm，tanθ＝4/3得，

B′O的长为40cm． 在直角三角形中，由三角形的边长条件得AB′＝50cm，但据题设条件AB＝50cm，故B′点与定滑轮的固定处B点重合，即得φ＝90°

（2）如图所示，选取坐标系，根据平衡条件有：

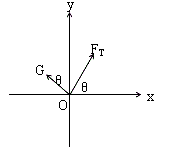
Gcosθ＋FTsinθ－mg＝0

FTcosθ－Gsinθ＝0．

即FT＝8N．

（3）圆环将要滑动时，得：

mGg＝FTcotθ，

mG＝0．6kg．