题目内容
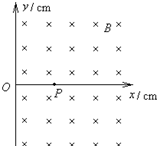 如图所示,在真空中坐标xOy面的x>0区域内,有磁感应强度B=0.20T的匀强磁场,方向与xOy平面垂直向里.在x轴上的P(10,0)点处有一放射源,在xOy平面内向各个方向发射速率为v=1.0×106m/s的带正电粒子,粒子的质量为m=6.4×10-27kg,粒子带电量为q=3.2×10-19C,不计粒子的重力,求:
如图所示,在真空中坐标xOy面的x>0区域内,有磁感应强度B=0.20T的匀强磁场,方向与xOy平面垂直向里.在x轴上的P(10,0)点处有一放射源,在xOy平面内向各个方向发射速率为v=1.0×106m/s的带正电粒子,粒子的质量为m=6.4×10-27kg,粒子带电量为q=3.2×10-19C,不计粒子的重力,求:(1)带电粒子在磁场中运动的轨道半径;
(2)y轴上能被带电粒子击中的最低和最高位置;
(3)打在y轴正向最远点的粒子,在磁场中运动的时间.
分析:(1)根据洛伦兹力提供向心力,由牛顿第二定律,即可求解;
(2)根据左手定则判断洛伦兹力方向,作出运动轨迹的图,由几何关系,即可求解;
(3)根据运动的周期公式,结合轨迹对应的圆心角,从而确定在磁场中运动的时间.
(2)根据左手定则判断洛伦兹力方向,作出运动轨迹的图,由几何关系,即可求解;
(3)根据运动的周期公式,结合轨迹对应的圆心角,从而确定在磁场中运动的时间.
解答:解:(1)洛仑兹力提供圆周运动向心力:qvB=m
解得轨道半径 r=
=
m=0.10m
(2)放射源射出粒子速度大小相同,因此在磁场中轨道半径相同,它们轨迹的圆心都在以P点为圆心r=10cm为半径的圆上,如图所示.
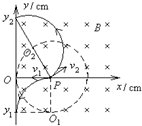
当轨道圆心在O1处时,粒子打在y轴的最低点:
y1=-r=-10cm
当轨道圆心在O2处时,粒子打在y轴的最高点:y2=
=
r=10
cm=17.3cm
(3)粒子在磁场中运动的周期 T=
打在y轴正向最远点的粒子,在磁场中运动的时间 t=
T
t=
=
s=3.14×10-7s
也可以是 t=
=
=3.14×10-7s
答:(1)带电粒子在磁场中运动的轨道半径0.1m;
(2)y轴上能被带电粒子击中的最低y1=-10cm和最高位置17.3cm;
(3)打在y轴正向最远点的粒子,在磁场中运动的时间3.14×10-7s.
| v2 |
| r |
解得轨道半径 r=
| mv |
| qB |
| 6.4×10-27×1.0×106 |
| 3.2×10-19×0.2 |
(2)放射源射出粒子速度大小相同,因此在磁场中轨道半径相同,它们轨迹的圆心都在以P点为圆心r=10cm为半径的圆上,如图所示.

当轨道圆心在O1处时,粒子打在y轴的最低点:
y1=-r=-10cm
当轨道圆心在O2处时,粒子打在y轴的最高点:y2=
| (2r)2-r2 |
| 3 |
| 3 |
(3)粒子在磁场中运动的周期 T=
| 2πm |
| qB |
打在y轴正向最远点的粒子,在磁场中运动的时间 t=
| 1 |
| 2 |
t=
| πm |
| qB |
| 3.14×6.4×10-27 |
| 3.2×10-19×0.2 |
也可以是 t=
| πr |
| v |
| 3.14×0.10 |
| 1.0×106 |
答:(1)带电粒子在磁场中运动的轨道半径0.1m;
(2)y轴上能被带电粒子击中的最低y1=-10cm和最高位置17.3cm;
(3)打在y轴正向最远点的粒子,在磁场中运动的时间3.14×10-7s.
点评:考查粒子在洛伦兹力作用下,做匀速圆周运动,掌握牛顿第二定律的应用,理解几何关系与运动半径联系,掌握由周期与圆心角来确定运动的时间方法.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
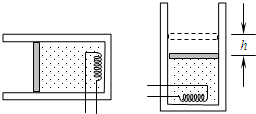 [选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若三题都做,则按A、B两题评分.
[选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若三题都做,则按A、B两题评分.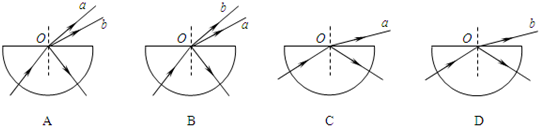
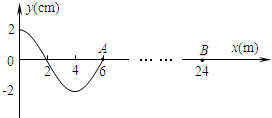
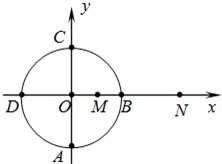 如图所示,真空中xOy光滑绝缘水平面内,在坐标点M(L,0)固定一个点电荷-Q,坐标点N(4L,0)固定一个点电荷+2Q,以O点为圆心,半径为2L的圆与坐标轴的交点分别为A、B、C、D.已知若取无穷远处电势为零,则离点电荷Q距离为r处的电势为φ=k
如图所示,真空中xOy光滑绝缘水平面内,在坐标点M(L,0)固定一个点电荷-Q,坐标点N(4L,0)固定一个点电荷+2Q,以O点为圆心,半径为2L的圆与坐标轴的交点分别为A、B、C、D.已知若取无穷远处电势为零,则离点电荷Q距离为r处的电势为φ=k [选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若三题都做,则按A、B两题评分.
[选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若三题都做,则按A、B两题评分.

