题目内容
（18分）（注意在试卷上作答无效）
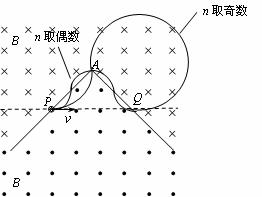
如图所示，空间某平面内有一条折线是磁场的分界线，在折线的两侧分布着方向相反、与平面垂直的匀强磁场，磁感应强度大小都为B。折线的顶角∠A＝90°，P、Q是折线上的两点， AP=AQ=L。现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出，不计微粒的重力。求：
⑴若在P、Q间加一与磁场方向垂直的匀强电场，能使速度为v0射出的微粒沿PQ直线运动到Q点，则场强为多大？
⑵撤去电场，为使微粒从P点射出后，途经折线的顶点A而到达Q点，求初速度v应满足什么条件？
⑶求第（2）问中微粒从P点到达Q点所用的时间。
（18分）
⑴由电场力与洛伦兹力平衡得：qE=qv0B
得：E=v0B （３分）
（2）根据运动的对称性，微粒能从P点到达Q点，
应满足应满足 
（４分）
又 
（2分）
由①②③式得：
，n=1、2、3、…… （2分）
（3）T=
（1分）
当n取奇数时
t=nT =n ，其中n=1、3、5、…… （3分）
当n取偶数时， t=2n
=n
其中n=2、4、6、…… （3分）
练习册系列答案
阅读快车系列答案
相关题目
。一根质量为m的导体棒AB在电机牵引下，以恒定速度v0沿OH方向从斜面底端开始运动，滑上导轨并到达斜面顶端， AB⊥OH。金属导轨的CD、FG段电阻不计，DEF段与AB棒材料横截面积均相同，单位长度的电阻均为r，O是AB棒的中点，整个斜面处在垂直斜面向上、磁感应强度为B的匀强磁场中。求：
