题目内容
【题目】如图，由某种粗细均匀的总电阻为
的金属条制成的矩形线框abcd，固定在水平面内且处于方向竖直向下的匀强磁场B=1T中。一接入电路电阻为
的导体棒PQ，长度为L=0.5m在水平拉力作用下沿ab、dc以速度v=1m/s匀速滑动，滑动过程PQ始终与ab垂直，且与线框接触良好，不计摩擦。在PQ从靠近ad处向bc滑动的过程中：（）
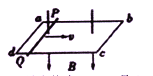
A. PQ两点间电势差绝对值的最大值为0.5V，且P、Q两点电势满足
B. 导体棒PQ产生的感应电动势为0.5V，电流方向从Q到P
C. 线框消耗的电功率先增大后减小
D. 线框消耗的电功率先减小后增大
【答案】BC
【解析】根据数学知识可知,当PQ位于中点时,外电阻最大,最大值为：R外=40×
×=10
；
AB.导体棒由靠近ad边向bc边匀速滑动的过程中，产生的感应电动势E=BLv=0.5V，保持不变，外电路总电阻先增大后减小，PQ中电流先减小后增大，PQ两端电压为路端电压，由U=EIR，可知PQ两端的电压先增大后减小，当导体棒运动到中点时，电压最大，最大电压为
。由右手定则可以判断，电流方向从Q到P，故A错误，B正确；
CD. 线框作为外电路,总电阻最大值为R外=10，等于内阻，从最左端达到中间位置的过程中，导体棒PQ上的电阻先大于线框的外电阻，达到中点位置时等于线框外电阻，再移动再大于线框的外电阻，线框消耗的电功率先增大后减小，故C正确，D错误。
故选：BC.
练习册系列答案
阅读快车系列答案
相关题目
