题目内容
14.一座高度未知的塔,从塔顶由静止释放一个石块A,当它下落到离塔顶2m时,又从距离塔顶6m高处由静止释放另一石块B,最终发现两石块同时落地.若不计空气阻力,则塔高是多少?(重力加速度g=10m/s2)分析 设B石块自由下落的时间为t,求出此时石块A的速度,抓住石块B的位移加上6m6等于塔高,以及石块A在t内的位移加上2等于塔高.接触时间t,从而求出塔高.
解答 解:设B石块自由下落的时间为t,此时A石块的速度v=$\sqrt{2×10×2}=2\sqrt{10}$m/s.
设B石块自由下落的时间为t,A与B的位移关系:$\frac{1}{2}g{t}^{2}+6=2+vt+\frac{1}{2}g{t}^{2}$
解得:t=$\frac{\sqrt{10}}{5}$s
则塔高:h=$\frac{1}{2}g{t}^{2}+6=\frac{1}{2}×10×(\frac{\sqrt{10}}{5})^{2}+6$=8m
答:塔高是8m.
点评 解决本题的关键掌握自由落体运动的位移时间公式h=$\frac{1}{2}g{t}^{2}$,以及抓住两石块同时落地.

练习册系列答案
相关题目
4.关于质点,下列说法中正确的是( )
| A. | 转动的物体一定不能看成质点 | |
| B. | 因为质点没有大小,所以与几何中的点没有区别 | |
| C. | 研究运动员在5 000米长跑比赛中运动的快慢时,可以把运动员看成质点 | |
| D. | 研究跳水运动员在空中的翻转动作,可以把运动员看成质点 |
5.物体从高H处自由落下,空气阻力忽略不计,落地速度为v,则当它下落$\frac{H}{4}$时的速度为( )
| A. | $\frac{v}{4}$ | B. | $\frac{\sqrt{gH}}{4}$ | C. | $\frac{\sqrt{2gH}}{2}$ | D. | $\frac{v}{2}$ |
2.下列说法中正确的是( )
| A. | 只有体积很小的物体才能被看成质点 | |
| B. | 第3s表示时刻 | |
| C. | 选取不同的参考系,所得出的关于物体运动的结论可能是不同的 | |
| D. | 在田径场1500m长跑比赛中,跑完全程的运动员的位移大小为1500m |
19.关于重力下列说法正确的是( )
| A. | 自由下落的物体不受重力 | B. | 重力就是地球对物体的吸引力 | ||
| C. | 重力的方向总是竖直向下 | D. | 重心是物体上最重的点 |
6.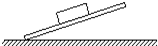 物体静止在斜面上,若斜面倾角缓慢减小,则物体受到斜面的支持力和摩擦力的变化情况是( )
物体静止在斜面上,若斜面倾角缓慢减小,则物体受到斜面的支持力和摩擦力的变化情况是( )
 物体静止在斜面上,若斜面倾角缓慢减小,则物体受到斜面的支持力和摩擦力的变化情况是( )
物体静止在斜面上,若斜面倾角缓慢减小,则物体受到斜面的支持力和摩擦力的变化情况是( )| A. | 支持力增大,摩擦力减小 | B. | 支持力减小,摩擦力增大 | ||
| C. | 支持力增大,摩擦力增大 | D. | 支持力减小,摩擦力减小 |
