题目内容
 (2011?抚州模拟)如图所示,劲度系数为k的轻弹簧,左端连着绝缘介质小球B,右端连在固定板上,放在光滑绝缘的水平面上.整个装置处在场强大小为E、方向水平向右的匀强电场中.现有一质量为m、带电荷量为+q的小球A,从距B球为S处自由释放,并与B球发生碰撞.碰撞中无机械能损失,且A球的电荷量始终不变.已知B球的质量M=3m,B球被碰后作周期性运动,其运动周期T=2π
(2011?抚州模拟)如图所示,劲度系数为k的轻弹簧,左端连着绝缘介质小球B,右端连在固定板上,放在光滑绝缘的水平面上.整个装置处在场强大小为E、方向水平向右的匀强电场中.现有一质量为m、带电荷量为+q的小球A,从距B球为S处自由释放,并与B球发生碰撞.碰撞中无机械能损失,且A球的电荷量始终不变.已知B球的质量M=3m,B球被碰后作周期性运动,其运动周期T=2π
|
(1)求A球与B球第一次碰撞后瞬间,A球的速度V1和B球的速度V2;
(2)要使A球与B球第二次仍在B球的初始位置迎面相碰,求劲度系数k的可能取值.
分析:(1)两球发生弹性碰撞时满足动量守恒定律和机械能守恒定律,记住碰后两球速度的表达式;
(2)A球碰后先向左减速再反向加速两次时间相等,B球从碰后再回到原位置的时间具有周期性,二者相等即可求解.
(2)A球碰后先向左减速再反向加速两次时间相等,B球从碰后再回到原位置的时间具有周期性,二者相等即可求解.
解答:解:(1)设A球与B球碰撞前瞬间的速度为v0,由动能定理得,qES=
m
①
解得:
=
②
碰撞过程中动量守恒得 m
=m
+M
③
机械能无损失,有
m
=
m
+
M
④
联立解得
=-
( 负号表示方向向左),
=
,方向向右
即A球与B球第一次碰撞后瞬间,A球的速度V1大小为解得
,方向向左;B球的速度V2大小为
,方向向右.
(2)要使m与M第二次迎面碰撞仍发生在原位置,则必有A球重新回到O处所用的时间t恰好等于B球周期的(n+
),即t=(n+
)T,其中n=0,1,2,3…
对A由a=
及
=at可求出A球回到原碰撞点的时间t=
,所以有
=nT+
(n=0,1,2,3…)
将T=2π
、
=
及a=
代入上式可得K=
(n=0,1,2,3,…)
即要使A球与B球第二次仍在B球的初始位置迎面相碰,劲度系数k的可能取值为K=
(n=0,1,2,3,…)
| 1 |
| 2 |
| v | 2 0 |
解得:
| v | 0 |
|
碰撞过程中动量守恒得 m
| v | 0 |
| v | 1 |
| v | 2 |
机械能无损失,有
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
联立解得
| v | 1 |
| 1 |
| 2 |
|
| v | 2 |
| 1 |
| 2 |
|
即A球与B球第一次碰撞后瞬间,A球的速度V1大小为解得
| 1 |
| 2 |
|
| 1 |
| 2 |
|
(2)要使m与M第二次迎面碰撞仍发生在原位置,则必有A球重新回到O处所用的时间t恰好等于B球周期的(n+
| 1 |
| 2 |
| 1 |
| 2 |
对A由a=
| Eq |
| m |
| v | 1 |
| ||
| a |
| ||
| a |
| T |
| 2 |
将T=2π
|
| v | 1 |
| 1 |
| 2 |
|
| Eq |
| m |
| ||||
| 2S |
即要使A球与B球第二次仍在B球的初始位置迎面相碰,劲度系数k的可能取值为K=
| ||||
| 2S |
点评:质量为
的小球以
与静止的质量为
的小球发生弹性碰撞,根据动量守恒定律和机械能守恒定律联立可得碰后两球速度分别为
=
,
=
;要重视对物理过程的分析和训练,注意弹簧振子运动的周期性.
| m | 1 |
| v | 1 |
| m | 2 |
| v | ′ 1 |
| ||||
|
| .v | 1 |
| v | ′ 2 |
| ||||
|
| .v | 1 |

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 (2011?抚州模拟)如图所示,小球从光滑的圆弧轨道下滑至水平轨道末端时,光电装置被触动,控制电路会使转筒立刻以某一角速度匀速连续转动起来.转筒的底面半径为R,已知轨道末端与转筒上部相平,与转筒的转轴距离为L,且与转筒侧壁上的小孔的高度差为h;开始时转筒静止,且小孔正对着轨道方向.现让一小球从圆弧轨道上的某处无初速滑下,若正好能钻入转筒的小孔(小孔比小球略大,小球视为质点,不计空气阻力,重力加速度为g),求:
(2011?抚州模拟)如图所示,小球从光滑的圆弧轨道下滑至水平轨道末端时,光电装置被触动,控制电路会使转筒立刻以某一角速度匀速连续转动起来.转筒的底面半径为R,已知轨道末端与转筒上部相平,与转筒的转轴距离为L,且与转筒侧壁上的小孔的高度差为h;开始时转筒静止,且小孔正对着轨道方向.现让一小球从圆弧轨道上的某处无初速滑下,若正好能钻入转筒的小孔(小孔比小球略大,小球视为质点,不计空气阻力,重力加速度为g),求: (2011?抚州模拟)图为一横波发生器的显示屏,可以显示出波由0点从左向右传播的图象,
(2011?抚州模拟)图为一横波发生器的显示屏,可以显示出波由0点从左向右传播的图象, (2011?抚州模拟)如图所示,匀强磁场中有一个电荷量为q的正离子,自a点沿半圆轨道运动,当它运动到b点时,突然吸收了附近若干电子,接着沿另一半圆轨道运动到c点,已知a、b、c在同一直线上,且ab=2ac,电子电荷量为e,电子质量可忽略不计,则该离子吸收的电子个数为( )
(2011?抚州模拟)如图所示,匀强磁场中有一个电荷量为q的正离子,自a点沿半圆轨道运动,当它运动到b点时,突然吸收了附近若干电子,接着沿另一半圆轨道运动到c点,已知a、b、c在同一直线上,且ab=2ac,电子电荷量为e,电子质量可忽略不计,则该离子吸收的电子个数为( )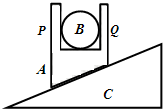 (2011?抚州模拟)如图所示,带有长方体盒子的斜劈A放在固定的斜面体C的斜面上,在盒子内放有光滑球B,B恰与盒子前、后壁P、Q点相接触.若使斜劈A在斜面体C上静止不动,则P、Q对球B无压力.以下说法不正确的是( )
(2011?抚州模拟)如图所示,带有长方体盒子的斜劈A放在固定的斜面体C的斜面上,在盒子内放有光滑球B,B恰与盒子前、后壁P、Q点相接触.若使斜劈A在斜面体C上静止不动,则P、Q对球B无压力.以下说法不正确的是( )