题目内容
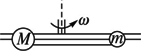
 如图所示,在光滑的以角速度ω旋转的细杆上穿有质量分别为m和M的两球,两球用轻细线连接,若M>m,则( )
如图所示,在光滑的以角速度ω旋转的细杆上穿有质量分别为m和M的两球,两球用轻细线连接,若M>m,则( )分析:两小球所受的绳子的拉力提供向心力,并且它们的加速度相等,根据向心力公式即可求解.
解答:解:A、两小球所受的绳子的拉力提供向心力,所以向心力大小相等,角速度又相等,当两球离轴距离相等时,则有:Mω2r>mω2r,所以两球相对杆会滑动.故A错误;
B、两球的向心力是相等的,得:Mω2r1=mω2r2 ,所以:
=
<1,两球离轴距离之比与质量成反比.所以两球离轴距离之比等于质量之比时,两球相杆都动.故B正确;
C、根据向心力的表达式,得:Mω2r1=mω2r2 ,;由于两球的向心力相等与角速度无关,所以转速为ω时,两球相对杆都不动,那么转速为2ω时两球也不动.故C正确;
D、由于两球用轻细线连接,所以两球相对杆滑动时,只能向同一方向滑动.故D错误;
故选:BC
B、两球的向心力是相等的,得:Mω2r1=mω2r2 ,所以:
| r1 |
| r2 |
| m |
| M |
C、根据向心力的表达式,得:Mω2r1=mω2r2 ,;由于两球的向心力相等与角速度无关,所以转速为ω时,两球相对杆都不动,那么转速为2ω时两球也不动.故C正确;
D、由于两球用轻细线连接,所以两球相对杆滑动时,只能向同一方向滑动.故D错误;
故选:BC
点评:本题主考考查了向心力公式的应用,知道两小球的角速度和向心力相等.

练习册系列答案
相关题目
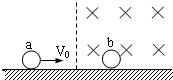 如图所示,在光滑的绝缘水平面上,有直径相同的两个金属球a和b,质量分别为ma=2m,mb=m,b球带正电荷2q,静止在磁感强度为B的匀强磁场中.原来不带电的a球以速度V0进入磁场与b球发生正碰.若碰后b球对桌面压力恰好为零,求a球对桌面压力是多大?
如图所示,在光滑的绝缘水平面上,有直径相同的两个金属球a和b,质量分别为ma=2m,mb=m,b球带正电荷2q,静止在磁感强度为B的匀强磁场中.原来不带电的a球以速度V0进入磁场与b球发生正碰.若碰后b球对桌面压力恰好为零,求a球对桌面压力是多大?