题目内容
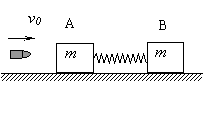
 在光滑水平面上放着两块质量都是m的木块A和B,中间用一根劲度倔强系数为k的轻弹簧连接着,如图,现从水平方向射来一颗子弹,质量为m/4,速度为v0,射中木块A后留在其中.
在光滑水平面上放着两块质量都是m的木块A和B,中间用一根劲度倔强系数为k的轻弹簧连接着,如图,现从水平方向射来一颗子弹,质量为m/4,速度为v0,射中木块A后留在其中.求:①在击中A瞬间木块A和B的速度分别为多少?
②在以后运动中弹簧的最大弹性势能是多少?
③在以后运动中A的最小速度和B的最大速度分别是多少?
分析:①在子弹击中A瞬间,弹簧没有发生发生形变,B的速度没有发生变化.对子弹和A组成的系统,由动量守恒列方程求解.
②当子弹、A和B三者共速时,弹性势能最大.对三者组成的系统用动量守恒和机械能守恒列两个方程,解方程组即可.
③当弹簧恢复原长时,A速度最小,B速度最大.对三者组成的系统用动量守恒和机械能守恒列两个方程,解方程组即可.
②当子弹、A和B三者共速时,弹性势能最大.对三者组成的系统用动量守恒和机械能守恒列两个方程,解方程组即可.
③当弹簧恢复原长时,A速度最小,B速度最大.对三者组成的系统用动量守恒和机械能守恒列两个方程,解方程组即可.
解答:解:①在子弹击中A瞬间,弹簧没有发生发生形变,B的速度没有发生变化.故vB=0.
对子弹和A,由系统的动量守恒得:
mv0=(
+m)vA,
解得:vA=
mv0;
②当三者共速时,弹性势能最大.
对系统,由系统动量守恒得:
mvA=(
m+m)v1,
由机械能守恒得:
(
m)vA2=Epm+
(
m)v12,
解得v1=
v0,Epm=
mv02;
③当弹簧恢复原长时,A速度最小,B速度最大.
由系统动量守恒得:(
m+m)v1=
mv2+mv3,
由机械能守恒得:
(m+
m)vA2=
(
m)v22+
mv32,
解得:v2=
v0,v3=
v0;
答:①在击中A瞬间木块A的速度为
v0,B的速度为0.②在以后运动中弹簧的最大弹性势能为
mv02;③在以后运动中A的最小速度为
v0,B的最大速度为
v0.
对子弹和A,由系统的动量守恒得:
| 1 |
| 4 |
| m |
| 4 |
解得:vA=
| 1 |
| 5 |
②当三者共速时,弹性势能最大.
对系统,由系统动量守恒得:
| 5 |
| 4 |
| 5 |
| 4 |
由机械能守恒得:
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
解得v1=
| 1 |
| 9 |
| 1 |
| 90 |
③当弹簧恢复原长时,A速度最小,B速度最大.
由系统动量守恒得:(
| 5 |
| 4 |
| 5 |
| 4 |
由机械能守恒得:
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
解得:v2=
| 1 |
| 45 |
| 2 |
| 9 |
答:①在击中A瞬间木块A的速度为
| 1 |
| 5 |
| 1 |
| 90 |
| 1 |
| 45 |
| 2 |
| 9 |
点评:此题有一定的难度,要求能根据物体的运动过程,分析得出临界状态所对应的临界条件:当子弹、A和B三者共速时,弹性势能最大.当弹簧恢复原长时,A速度最小,B速度最大.此题属于难题.

练习册系列答案
相关题目
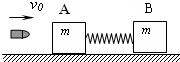 (1)下列叙述正确的有
(1)下列叙述正确的有