Question

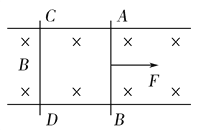
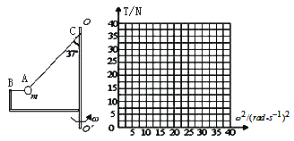
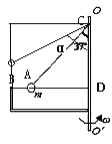
【题目】如图，装置BOO′可绕竖直轴OO′转动，可视为质点的小球A与两细线连接后分别系于B、C两点，装置静止时细线AB水平，细线AC与竖直方向的夹角θ=37.已知小球的质量，细线AC长L＝1m，B点距转轴的水平距离和距C点的竖直距离相等.（g取10m/s2，sin37=0.6，cos37=0.8）

（1）若装置匀速转动的角速度为时，细线AB水平拉直且张力为0，求角速度的大小；

（2）若装置匀速转动的角速度为时，细线AB刚好竖直且张力为0，求角速度的大小；

（3）装置可以以不同的角速度匀速转动，试通过计算在坐标系中作出细线AC中张力T与角速度的平方之间的关系图像．

Answer 1

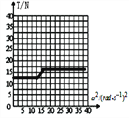
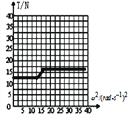
【答案】（1）3.54（rad/s）（2）4.08（rad/s）（3）T-ω2图像如图：

【解析】如图所示，由题意得：Lcosθ=AB+Lsinθ

得AB=0.2m

（1）当水平方向TB=0时，对小球由牛顿第二定律得：

得：ω1=（rad/s）

（2）当竖直方向TB=0时，对小球由牛顿第二定律得：

得：ω1=（rad/s）

（3）当rad/s时，对小球有：

得：T=mg/cosθ=12.5N

当时，对小球由牛顿第二定律有：

得：T=mLω2

当rad/s时，对小球有：

得：得：T=mLω2

T-ω2图像如图：