题目内容
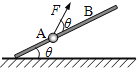
【题目】如图所示，位于竖直平面内的光滑轨道，由一段斜的直轨道与之相切的圆形轨道连接而成，圆形轨道的半径为R．一质量为m的小物块（视为质点）从斜轨道上某处由静止开始下滑，然后沿圆形轨道运动．（g为重力加速度）
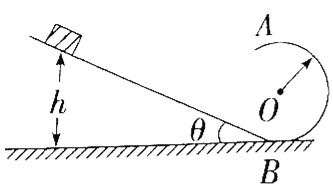
（1）要使物块能恰好通过圆轨道最高点，求物块初始位置相对于圆形轨道底部的高度h多大；
（2）要求物块能通过圆轨道最高点，且在最高点与轨道间的压力不能超过5mg．求物块初始位置相对于圆形轨道底部的高度h的取值范围．
【答案】（1）
；（2）
【解析】试题分析：根据牛顿第二定律求得在A处的速度，然后应用机械能守恒求得高度；根据牛顿第二定律求得在A处的速度范围，然后应用机械能守恒求得高度取值范围；
（1）要使物块能恰好通过圆轨道最高点，那么对物块在最高点A处应用牛顿第二定律可得
．
又有物块运动过程只有重力做功，机械能守恒，所以有
所以
．
（2）要求物块能通过圆轨道最高点，且在最高点与轨道间的压力不能超过5mg，那么由牛顿第三定律可得：物块在最高点受到轨道的支持力不超过5mg．
所以，对物块在最高点A处应用牛顿第二定律可得： 
．
又有物块运动过程只有重力做功，机械能守恒，所以有
．
所以， 
，所以
．
学练快车道快乐假期寒假作业系列答案【题目】小明同学在做“互成角度的两个力的合成”实验时，利用坐标纸记下了橡皮筋的结点位置O点以及两只弹簧测力计拉力的大小，如图（a）所示．
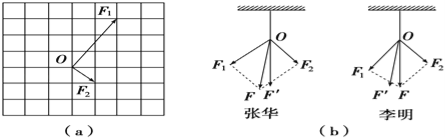
（1）试在图（a）中作出无实验误差情况下F1和F2的合力图示，并用F表示此力．
（2）有关此实验，下列叙述正确的是 ．
A．两弹簧测力计的拉力可以同时比橡皮筋的拉力大 |
B．橡皮筋的拉力是合力，两弹簧测力计的拉力是分力 |
C．两次拉橡皮筋时，需将橡皮筋结点拉到同一位置O，这样做的目的是保证两次弹簧测力计拉力的效果相同 |
D．若只增大某一只弹簧测力计的拉力大小而保证橡皮筋结点位置不变，只需调整另一只弹簧测力计拉力的大小即可 |
（3）如图（b）所示是李明和张华两位同学在做以上实验时得到的结果，其中哪一个实验比较符合实验事实？（力F′是用一只弹簧测力计拉时的图示） ．（填李明或张华）
