题目内容
 (2008?徐州三模)光滑的水平轨道AB,与半径为R的光滑的半圆形轨道BCD相切于B点,其中圆轨道在竖直平面内,B为最低点,D为最高点.一质量为m的小球以初速度v0沿AB运动,恰能通过最高点,则( )
(2008?徐州三模)光滑的水平轨道AB,与半径为R的光滑的半圆形轨道BCD相切于B点,其中圆轨道在竖直平面内,B为最低点,D为最高点.一质量为m的小球以初速度v0沿AB运动,恰能通过最高点,则( )分析:小球恰能通过最高点时,由重力提供向心力,根据牛顿第二定律求出小球经最高点时的速度,根据动能定理求出初速度v0与半径R的关系.小球经过B点后的瞬间由重力和轨道的支持力的合力提供向心力,由牛顿运动定律研究小球对轨道的压力与半径的关系.
解答:解:
A、C小球恰能通过最高点时,则有mg=
,vD=
,根据动能定理得,
m
=
m
+2mgR,得到v0=
,可见,R越大,v0越大,而且v0与小球的质量m无关.故A正确,C错误.
B、小球经过B点后的瞬间,N-mg=m
,得到轨道对小球的支持力N=mg+m
,R越大,N越小,小球经过B点后的瞬间对轨道的压力也越小.故B错误.
D、初动能Ek0=
m
=
m
+2mgR=
mgR,得知m与R同时增大,初动能Ek0增大.故D正确.
故选AD
A、C小球恰能通过最高点时,则有mg=
| ||
| R |
| gR |
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 D |
| 5gR |
B、小球经过B点后的瞬间,N-mg=m
| ||
| R |
| ||
| R |
D、初动能Ek0=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 D |
| 5 |
| 2 |
故选AD
点评:动能定理与向心力知识综合是常见的题型.小球恰好通过最高点时速度与轻绳模型类似,轨道对小球恰好没有作用力,由重力提供向心力,临界速度v=
,做选择题时可直接运用.
| gR |

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
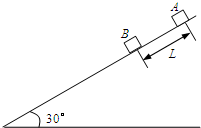 (2008?徐州三模)如图所示,在倾角θ=30°、足够长的斜面上分别固定着两个物体A.B,相距L=0.2m,它们的质量mA=mB=1kg,与斜面间的动摩擦因数分别为
(2008?徐州三模)如图所示,在倾角θ=30°、足够长的斜面上分别固定着两个物体A.B,相距L=0.2m,它们的质量mA=mB=1kg,与斜面间的动摩擦因数分别为 (2008?徐州三模)质量为1kg的物体在水平面内做曲线运动,已知互相垂直方向上的速度图象分别如图所示.下列说法正确的是( )
(2008?徐州三模)质量为1kg的物体在水平面内做曲线运动,已知互相垂直方向上的速度图象分别如图所示.下列说法正确的是( ) (2008?徐州三模)如图所示,虚线框内存在着匀强电场(方向未知),一质子从bc边上的M点以速度v0射进电场内,最后从cd边上的Q点飞出电场.下列说法不正确的是( )
(2008?徐州三模)如图所示,虚线框内存在着匀强电场(方向未知),一质子从bc边上的M点以速度v0射进电场内,最后从cd边上的Q点飞出电场.下列说法不正确的是( ) (2008?徐州三模)如图所示为一理想变压器,原线圈匝数为n1,四个副线圈的匝数均为n2,四个副线圈中负载电阻的阻值相同,二极管为理想二极管.现从原线圈P、Q两端输入正弦交变电流,那么下列说法正确的是( )
(2008?徐州三模)如图所示为一理想变压器,原线圈匝数为n1,四个副线圈的匝数均为n2,四个副线圈中负载电阻的阻值相同,二极管为理想二极管.现从原线圈P、Q两端输入正弦交变电流,那么下列说法正确的是( )