题目内容
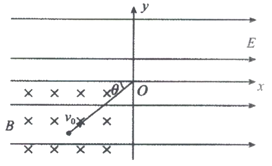
【题目】如图所示，竖直平面xOy，其x轴水平，在整个平面内存在沿x轴正方向的匀强电场E，在第三象限内有垂直纸面向里的匀强磁场，磁感应强度大小为B=0.2T。现有一比荷为
=25C/kg的带电微粒，从第三象限内某点以速度v0向坐标原点O做直线运动，v0与x轴之间的夹角为θ=45°，重力加速度g=10m/s2。求：
(1)微粒的电性及速度v0的大小；
(2)带电微粒在第一象限内运动时所达到最高点的坐标。
【答案】（1）
（2）（0.6m，0.2m）
【解析】
解：(1)带电粒子在第三象限内做直线运动，受到重力、电场力和洛伦兹力三个力的作用，并且合力为零，即粒子做匀速直线运动；所以，微粒受到的洛伦兹力垂直于速度方向斜向左上方，由左手定则可判断为零带正电；
对带电微粒受力分析，如图所示，根据平衡条件可得：
解得：
(2)带电微粒进入第一象限后做曲线运动，假设最高点为M点，从O到M点所用的时间为t，则将微粒从O到M的运动分解为沿x轴方向的匀加速直线运动和沿y轴方向上的匀减速直线运动
Y轴方向：
x轴方向上：
解得
，
练习册系列答案
相关题目
