题目内容
（2013?宁波模拟）如图所示，速度不同的同种带电粒子（重力都不计）a、b沿半径．AO方向进入一圆形匀强磁场区域，a、b两粒子的运动轨迹分别为AB和AC，则下列说法中正确的是（ ）分析：由运动轨迹可比较半径，由于半径利用洛伦兹力提供向心力可比较速度；
由圆周运动可得周期表达式，进而判定运动时间；
圆的对称性可以知道，离开磁场时，速度一定背离圆心；
由圆周运动可得周期表达式，进而判定运动时间；
圆的对称性可以知道，离开磁场时，速度一定背离圆心；
解答：解：
A、由运动轨迹可知，a的半径小于b的半径，粒子在磁场中洛伦兹力提供向心力，做匀速圆周运动．则有Bqv=m
得：v=
，由于带电粒子们的B、q、m均相同，所以v与r成正比，可知a粒子的速度比b粒子速度小，故A错误．
B、由周期公式得：T=
，由于带电粒子们的B、q、m均相同，所以T均相同，由于a的圆心角大，故a在磁场中的运动时间长，故B正确．
CD、进入磁场区域时，速度方向指向圆心O，根据圆的对称性可以知道，离开磁场时，速度一定背离圆心，故C正确，D错误．
故选：BC
A、由运动轨迹可知，a的半径小于b的半径，粒子在磁场中洛伦兹力提供向心力，做匀速圆周运动．则有Bqv=m
| v2 |
| r |
| Bqr |
| m |
B、由周期公式得：T=
| 2πm |
| qB |
CD、进入磁场区域时，速度方向指向圆心O，根据圆的对称性可以知道，离开磁场时，速度一定背离圆心，故C正确，D错误．
故选：BC
点评：本题关键是结合圆的对称性来分析运动轨迹，其次要熟练掌握洛伦兹力提供向心力列式分析计算．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
（2013?宁波模拟）如图所示电路中，电源电动势为E，线圈L的直流电阻不计，以下判断正确的是（ ）
（2013?宁波模拟）如图所示，固定在地面上的半圆轨道直径ab水平，质点P与半圆轨道的动摩擦因数处处一样，当质点P从a点正上方高H处自由下落，经过轨道后从b点冲出竖直上抛，上升的最大高度为H/2，空气阻力不计．当质点下落再经过轨道a点冲出时，能上升的最大高度h为（ ）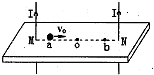
（2013?宁波模拟）如图所示，两根长直导线竖直插入光滑绝缘水平桌面上的M、N两小孔中，O为M、N连线中点，连线上a、b两点关于O点对称．导线均通有大小相等、方向向上的电流．已知长导线在周围产生的磁场的磁感应强度B=