��Ŀ����
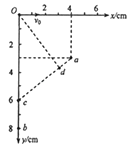
����Ŀ����ͼ��ʾ����ֱ������ϵxOyƽ������a��4cm��3cm����b��0��8cm�����㣬��ǿ�ų���ֱ��xOyƽ�����һ�����Ϊe=1.6��10��19C������Ϊm=9��10��31kg�ĵ��ӣ���v0=1.6��106m/s���ٶȴ�ԭ��O��x�����������䣬���Ƶ���������ȡsin37��=0.6��
��1����֪������ͨ��a����Ÿ�Ӧǿ��B�Ĵ�С��
��2���ʵ��ı�Ÿ�Ӧǿ�ȣ��ټ���ƽ��xOyƽ�����ǿ�糡��ʹ�õ��ӿ��Ⱥ�a��b���㣬���ֱܷ�Ϊ��O�㶯�ܵ�4����5������糡ǿ�ȣ�
���𰸡�
��1��
�⣺����������Բ���˶����ɼ��ι�ϵ���У�
![]() ��
��
��ã�R= ![]() cm��
cm��
����ţ�ٵڶ����ɣ��У� ![]()
��ã�B=2.16��10��4T
��2��
�⣺�������������������Ӵ�O�㵽a���ɶ��ܶ������У�
![]() ��
��
���Ӵ�O�㵽b�㣬�ɶ��ܶ������У�
![]()
��ã� ![]()
����ob������ƾ������ߣ���y���ϵ�c��0��yc��Ϊa��ĵ��Ƶ㣺
![]()
��ã�yc=6cm��ac����Ϊ��ǿ�糡�е�һ�������ߣ�
��O����ac�Ĵ��߽���d�㣬�ɼ��ι�ϵ��֪��
��cOd=37��
O�㵽d����룺
Od=yc��cos37��
E= ![]()
�������ݽ�ã�E=450V/m
������y�Ḻ�����37�㣬��dָ��O�ķ���ƽ��
����������1�����Ӵ�ֱ������ǿ�ų���������Բ���˶�����ϼ��ι�ϵ�õ�����뾶������ţ�ٵڶ�������ʽ���Ÿ�Ӧǿ�ȵĴ�С����2������������������ֻ�е糡�����������ݶ��ܶ����õ�ao���ѹ��bo���ѹ�ı�ֵ����ż��ϼ��ι�ϵ������U=Ed��ʽ������
�����㾫����������Ĺؼ���������ܶ�������������֪ʶ�����ն��ܶ����ı���ʽ���������ܺ�����������ֱ���˶�������µó���.����Ҳ�����ڱ����������������˶�����������Ͷ��ܶ��DZ�������������ʸ������ֽ⣬�ʶ��ܶ�������ʽ���Լ����������������⣬�˽���������ʼ�մ�ֱ��v�ķ���������������һ����������

 Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�����Ŀ����ͼ��ʾ����̽��Ħ������ʵ���У��õ��ɲ�����ˮƽ��һ����ˮƽ�����ϵ�Сľ�飬Сľ����˶�״̬�뵯�ɲ����ƵĶ������±���ʾ��ÿ��ʵ��ʱ��ľ��������ĽӴ�����ͬ�������±�������֪��������Щѡ������ȷ���ǣ� ��
ʵ����� | Сľ����˶�״̬ | ���ɲ����ƶ�����N�� |
1 | ��ֹ | 0.4 |
2 | ��ֹ | 0.6 |
3 | ֱ���� | 0.7 |
4 | ����ֱ�� | 0.5 |
5 | ֱ���� | 0.3 |
![]()
A.ľ���ܵ������Ħ����Ϊ0.7N
B.ľ���ܵ����Ħ��������Ϊ0.6N
C.�������ʵ���У�ľ���ܵ���Ħ������Сֻ����������ͬ��
D.�������ʵ���У�ľ���ܵ�Ħ������С������ͬ