题目内容
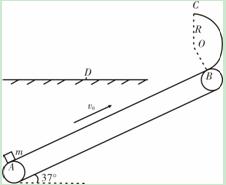
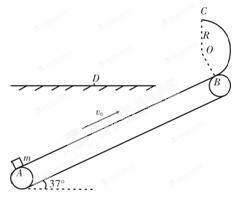
如图所示是一皮带传输装载机械示意图.井下挖掘工将矿物无初速放置于沿图示方向运行的传送带A端,被传输到末端B处,再沿一段圆形轨道到达轨道的最高点C处,然后水平抛到货台上.已知半径为R=0.4m的圆形轨道与传送带在B点相切,O点为半圆的圆心,BO、CO分别为圆形轨道的半径,矿物m可视为质点,传送带与水平面间的夹角θ=37°,矿物与传送带间的动摩擦因数μ=0.8,传送带匀速运行的速度为v=8m/s,传送带AB点间的长度为sAB=45m.若矿物落点D处离最高点C点的水平距离为sCD=2m,竖直距离为hCD=1.25m,矿物质量m=50kg,sin37°=0.6,cos37°=0.8,g=10m/s2,不计空气阻力.求:(1)矿物到达B点时的速度大小;
(2)矿物到达C点时对轨道的压力大小;
(3)矿物由B点到达C点的过程中,克服阻力所做的功.
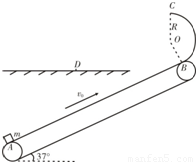
【答案】分析:(1)先假设矿物在AB段始终加速,根据动能定理求出矿物到达B点时的速度大小,将此速度与送带匀速运行的速度v=8m/s进行比较,确定假设是否合理.
(2)矿物从C到D过程做平抛运动,由平抛运动的规律求出经过C点时的速度大小,根据牛顿第二定律求得轨道对矿物的压力,即可得到矿物到达C点时对轨道的压力大小.
(3)矿物由B到C过程中,重力和阻力做功,由动能定理求解克服阻力所做的功.
解答:解:(1)假设矿物在AB段始终处于加速状态,由动能定理可得
(μmgcosθ-mgsinθ)=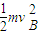
代入数据得 vB=6m/s
由于vB<v,故假设成立,矿物B处速度为6m/s.
(2)设矿物对轨道C处压力为F,由平抛运动知识可得
sCD=vCt
hCD=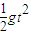
代入数据得矿物到达C处时速度vC=4m/s
由牛顿第二定律可得
F+mg=m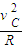
代入数据得 F=1500N
根据牛顿第三定律可得所求压力 F′=F=1500N
(3)矿物由B到C过程,由动能定理得
-mgR(1+cos37°)+Wf=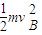 -
-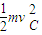
代入数据得 Wf=-140J
即矿物由B到达C时克服阻力所做的功是140J
答:(1)矿物到达B点时的速度大小是6m/s;
(2)矿物到达C点时对轨道的压力大小是1500N;
(3)矿物由B点到达C点的过程中,克服阻力所做的功是140J.
点评:本题主要考查了动能定理的应用及平抛运动的相关公式,要求同学们能根据题目要求选取不同的研究过程运用动能定理解题.
(2)矿物从C到D过程做平抛运动,由平抛运动的规律求出经过C点时的速度大小,根据牛顿第二定律求得轨道对矿物的压力,即可得到矿物到达C点时对轨道的压力大小.
(3)矿物由B到C过程中,重力和阻力做功,由动能定理求解克服阻力所做的功.
解答:解:(1)假设矿物在AB段始终处于加速状态,由动能定理可得
(μmgcosθ-mgsinθ)=
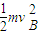
代入数据得 vB=6m/s
由于vB<v,故假设成立,矿物B处速度为6m/s.
(2)设矿物对轨道C处压力为F,由平抛运动知识可得
sCD=vCt
hCD=
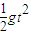
代入数据得矿物到达C处时速度vC=4m/s
由牛顿第二定律可得
F+mg=m
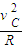
代入数据得 F=1500N
根据牛顿第三定律可得所求压力 F′=F=1500N
(3)矿物由B到C过程,由动能定理得
-mgR(1+cos37°)+Wf=
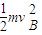 -
-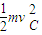
代入数据得 Wf=-140J
即矿物由B到达C时克服阻力所做的功是140J
答:(1)矿物到达B点时的速度大小是6m/s;
(2)矿物到达C点时对轨道的压力大小是1500N;
(3)矿物由B点到达C点的过程中,克服阻力所做的功是140J.
点评:本题主要考查了动能定理的应用及平抛运动的相关公式,要求同学们能根据题目要求选取不同的研究过程运用动能定理解题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 (2013?淄博一模)如图所示是一皮带传输装载机械示意图.井下挖掘工将矿物无初速放置于沿图示方向运行的传送带A端,被传输到末端B处,再沿一段圆形轨道到达轨道的最高点C处,然后水平抛到货台上.已知半径为R=0.4m的圆形轨道与传送带在B点相切,O点为半圆的圆心,BO、CO分别为圆形轨道的半径,矿物m可视为质点,传送带与水平面间的夹角θ=37°,矿物与传送带间的动摩擦因数μ=0.8,传送带匀速运行的速度为v0=8m/s,传送带AB点间的长度为sAB=45m.若矿物落点D处离最高点C点的水平距离为sCD=2m,竖直距离为hCD=1.25m,矿物质量m=50kg,sin37°=0.6,cos37°=0.8,g=10m/s2,不计空气阻力.求:
(2013?淄博一模)如图所示是一皮带传输装载机械示意图.井下挖掘工将矿物无初速放置于沿图示方向运行的传送带A端,被传输到末端B处,再沿一段圆形轨道到达轨道的最高点C处,然后水平抛到货台上.已知半径为R=0.4m的圆形轨道与传送带在B点相切,O点为半圆的圆心,BO、CO分别为圆形轨道的半径,矿物m可视为质点,传送带与水平面间的夹角θ=37°,矿物与传送带间的动摩擦因数μ=0.8,传送带匀速运行的速度为v0=8m/s,传送带AB点间的长度为sAB=45m.若矿物落点D处离最高点C点的水平距离为sCD=2m,竖直距离为hCD=1.25m,矿物质量m=50kg,sin37°=0.6,cos37°=0.8,g=10m/s2,不计空气阻力.求: