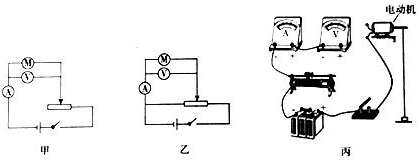
题目内容
5. 如图所示,两块长均为L的平行金属板M、N与水平面成α角放置在同一竖直平面,充电后板间有匀强电场.一个质量为m、带电量为q的液滴沿垂直于电场线方向以初速度v0射人电场,并沿虚线通过电场.则此电场的电场强度为多大?液滴离开电场时的速度为多大?
如图所示,两块长均为L的平行金属板M、N与水平面成α角放置在同一竖直平面,充电后板间有匀强电场.一个质量为m、带电量为q的液滴沿垂直于电场线方向以初速度v0射人电场,并沿虚线通过电场.则此电场的电场强度为多大?液滴离开电场时的速度为多大?
分析 (1)液滴在电场中受到重力和电场力作用,重力方向竖直向下,电场力方向垂直于两极板,两个力不在同一条直线上,故合力不为零.液滴沿直线运动,所以合力方向必定与液滴的运动方向同向或者反向,很明显在这合力应与物体的运动方向反向.电场力方向应垂直于虚线向上,此过程中电场力不做功,由平行四边形定则求解E;
(2)根据动能定理列式求解液滴离开电场时的速度.
解答  解:(1)由题液滴做直线运动,合力与该直线在同一直线上,则电场力方向应垂直于虚线向上,液滴所受的合力方向沿虚线向下.如图所示:
解:(1)由题液滴做直线运动,合力与该直线在同一直线上,则电场力方向应垂直于虚线向上,液滴所受的合力方向沿虚线向下.如图所示:
根据平衡条件,有:
qE=mgcosα
解得:E=$\frac{mgcosθ}{q}$
(2)因电场力与位移方向垂直,不做功,根据动能定理得:
-mgLsinθ=$\frac{1}{2}$mv2-$\frac{1}{2}$m${v}_{0}^{2}$
解得:v=$\sqrt{{v}_{0}^{2}-2gLsinθ}$
答:此电场的电场强度为$\frac{mgcosα}{q}$,液滴离开电场时的速度为$\sqrt{v_0^2-2glsinα}$.
点评 本题是带电体在复合场中运动的类型,分析液滴的受力情况,确定电场力的方向是解题的关键,要紧扣直线运动的条件进行分析.
第二问:(解法二)
带电液滴作直线运动,沿电场方向电场力和重力的分力相等.
即:Eq=mgcosα,匀减速运动加速度为a=gsinα,根据匀变速运动的公式${v^2}-v_0^2=2ax$,即可求出.

练习册系列答案
相关题目
19.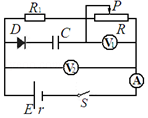 如图电路,C为电容器的电容,D为理想二极管(具有单向导通作用),电流表、电压表均为理想表.闭合开关S至电路稳定后,调节滑动变阻器滑片P向左移动一小段距离,结果发现电压表V1的示数改变量大小为△U1,电压表V2的示数改变量大小为△U2,电流表A的示数改变量大小为△I,则下列判断正确的有( )
如图电路,C为电容器的电容,D为理想二极管(具有单向导通作用),电流表、电压表均为理想表.闭合开关S至电路稳定后,调节滑动变阻器滑片P向左移动一小段距离,结果发现电压表V1的示数改变量大小为△U1,电压表V2的示数改变量大小为△U2,电流表A的示数改变量大小为△I,则下列判断正确的有( )
 如图电路,C为电容器的电容,D为理想二极管(具有单向导通作用),电流表、电压表均为理想表.闭合开关S至电路稳定后,调节滑动变阻器滑片P向左移动一小段距离,结果发现电压表V1的示数改变量大小为△U1,电压表V2的示数改变量大小为△U2,电流表A的示数改变量大小为△I,则下列判断正确的有( )
如图电路,C为电容器的电容,D为理想二极管(具有单向导通作用),电流表、电压表均为理想表.闭合开关S至电路稳定后,调节滑动变阻器滑片P向左移动一小段距离,结果发现电压表V1的示数改变量大小为△U1,电压表V2的示数改变量大小为△U2,电流表A的示数改变量大小为△I,则下列判断正确的有( )| A. | 滑片向左移动的过程中,电容器所带的电荷量不变 | |
| B. | $\frac{△{U}_{1}}{△I}$的值变大 | |
| C. | $\frac{△{U}_{2}}{△I}$的值不变,且始终等于电源内阻r | |
| D. | 滑片向左移动的过程中,电容器所带的电荷量要不断减少 |
20.下列关于闭合电路的说法中,错误的是( )
| A. | 电源短路时,路端电压等于电动势 | B. | 电源短路时,路端电压为零 | ||
| C. | 电源断路时,路端电压最大 | D. | 外电阻增大时,路端电压增大 |
17.物体在F1=5N水平拉力作用下沿粗糙水平面向右做匀速直线运动,某时刻撤去F1的同时施加F2=2N水平向左的拉力,则施加F2后瞬时,关于物体所受摩擦力大小和方向说法正确的是( )
| A. | 2N 方向水平向右 | B. | 5N 方向水平向左 | ||
| C. | 7N 方向水平向右 | D. | 3N 方向水平向左 |
10.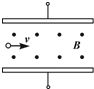 板长和板距之比为3:2的两块带电平行板之间有相互垂直的匀强磁场和匀强电场.质量为m、电荷量为q的带正电的粒子(重力不计),以速度v沿图示方向从中间进入.若撤掉电场,粒子恰好从极板边缘射出;若撤掉磁场,粒子也恰好从极板边缘射出;则磁感应强度和电场强度的大小之比B:E为( )
板长和板距之比为3:2的两块带电平行板之间有相互垂直的匀强磁场和匀强电场.质量为m、电荷量为q的带正电的粒子(重力不计),以速度v沿图示方向从中间进入.若撤掉电场,粒子恰好从极板边缘射出;若撤掉磁场,粒子也恰好从极板边缘射出;则磁感应强度和电场强度的大小之比B:E为( )
 板长和板距之比为3:2的两块带电平行板之间有相互垂直的匀强磁场和匀强电场.质量为m、电荷量为q的带正电的粒子(重力不计),以速度v沿图示方向从中间进入.若撤掉电场,粒子恰好从极板边缘射出;若撤掉磁场,粒子也恰好从极板边缘射出;则磁感应强度和电场强度的大小之比B:E为( )
板长和板距之比为3:2的两块带电平行板之间有相互垂直的匀强磁场和匀强电场.质量为m、电荷量为q的带正电的粒子(重力不计),以速度v沿图示方向从中间进入.若撤掉电场,粒子恰好从极板边缘射出;若撤掉磁场,粒子也恰好从极板边缘射出;则磁感应强度和电场强度的大小之比B:E为( )| A. | 9:10v | B. | 9:5v | C. | 9:10 | D. | 9:5 |
17.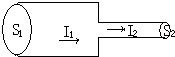 如图所示,一直流电路中的一段导体横截面示意图,其中S1:S2=4:1,I1、I2、U1、U2分别为通过两截面的电流及两截面单位长度上的电压.则( )
如图所示,一直流电路中的一段导体横截面示意图,其中S1:S2=4:1,I1、I2、U1、U2分别为通过两截面的电流及两截面单位长度上的电压.则( )
 如图所示,一直流电路中的一段导体横截面示意图,其中S1:S2=4:1,I1、I2、U1、U2分别为通过两截面的电流及两截面单位长度上的电压.则( )
如图所示,一直流电路中的一段导体横截面示意图,其中S1:S2=4:1,I1、I2、U1、U2分别为通过两截面的电流及两截面单位长度上的电压.则( )| A. | I1:I2=4:1; U 1:U2=4:1 | B. | I1:I2=1:1; U 1:U2=4:1 | ||
| C. | I1:I2=4:1; U 1:U2=1:4 | D. | I1:I2=1:1; U 1:U2=1:4 |
15. 如图示,电动势E内阻为r的电池与固定电阻R0 可变电阻R串联,如图所示,设R0=r,滑动变阻器最大电阻为2r,当滑动变阻器的滑片自a端向b端滑动时,下列各物理量随之增大的是( )
如图示,电动势E内阻为r的电池与固定电阻R0 可变电阻R串联,如图所示,设R0=r,滑动变阻器最大电阻为2r,当滑动变阻器的滑片自a端向b端滑动时,下列各物理量随之增大的是( )
 如图示,电动势E内阻为r的电池与固定电阻R0 可变电阻R串联,如图所示,设R0=r,滑动变阻器最大电阻为2r,当滑动变阻器的滑片自a端向b端滑动时,下列各物理量随之增大的是( )
如图示,电动势E内阻为r的电池与固定电阻R0 可变电阻R串联,如图所示,设R0=r,滑动变阻器最大电阻为2r,当滑动变阻器的滑片自a端向b端滑动时,下列各物理量随之增大的是( )| A. | 电池的输出功率 | B. | 变阻器消耗的功率 | ||
| C. | 固定电阻R0上消耗的功率 | D. | 电池内阻上消耗的功率 |
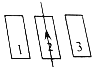 如图所示矩形线圈和通电直导线在同一平面内,在线框以平行于纸面不变的速度由位置1经位置2到达位置3的过程中.线框中感应电流的方向为先顺时针,再逆时针,最后又顺时针.
如图所示矩形线圈和通电直导线在同一平面内,在线框以平行于纸面不变的速度由位置1经位置2到达位置3的过程中.线框中感应电流的方向为先顺时针,再逆时针,最后又顺时针.