题目内容
波源S1和S2振动方向相同,频率均为4 Hz,分别置于均匀介质中x轴上的O?A两点处,OA="2" m,如图所示.两波源产生的简谐横波沿x轴相向传播,速度为4 m/s.已知两波源振动的初始相位相同.求:
(1)简谐横波的波长;
(2)OA间合振动振幅最小的点的位置.
(1)简谐横波的波长;
(2)OA间合振动振幅最小的点的位置.
(1)1 m (2)0.25 m,0.75 m,1.25 m,1.75 m
(1)设简谐横波的波长为λ,频率为ν,波速为v,则λ=
①
代入已知数据得λ="1" m.②
(2)以O为坐标原点,设P为OA间任意一点,其坐标为x,则两波源到P点的波程差
Δl=x-(2-x),0≤x≤2③,
其中x、Δl以m为单位,合振动的振幅最小的点的位置满足
Δl=(k+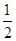
)λ,k为整数④,
联立③④式得x="0.25" m,0.75 m,1.25 m,1.75 m.
①代入已知数据得λ="1" m.②
(2)以O为坐标原点,设P为OA间任意一点,其坐标为x,则两波源到P点的波程差
Δl=x-(2-x),0≤x≤2③,
其中x、Δl以m为单位,合振动的振幅最小的点的位置满足
Δl=(k+
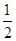)λ,k为整数④,联立③④式得x="0.25" m,0.75 m,1.25 m,1.75 m.
练习册系列答案
相关题目
