题目内容
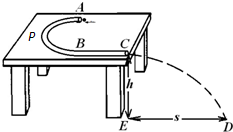
如图所示,轨道ABCD的AB段为一半径R=0.2 的光滑1/4圆形轨道,BC段为高为h=5
的光滑1/4圆形轨道,BC段为高为h=5 的竖直轨道,CD段为水平轨道。一质量为0.1
的竖直轨道,CD段为水平轨道。一质量为0.1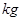 的小球由A点从静止开始下滑到B点时速度的大小为2
的小球由A点从静止开始下滑到B点时速度的大小为2 /s,离开B点做平抛运动(g取10
/s,离开B点做平抛运动(g取10 /s2),求:
/s2),求:
(1)小球离开B点后,在CD轨道上的落地点到C的水平距离
(2)小球到达B点时对圆形轨道的压力;
(3)如果在BCD轨道上放置一个倾角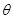 =45°的斜面(如图中虚线所示),那么小球离开B点后能否落到斜面上?如果能,求它第一次落在斜面上的位置。
=45°的斜面(如图中虚线所示),那么小球离开B点后能否落到斜面上?如果能,求它第一次落在斜面上的位置。
(1)2m;(2)3N;(3)1.13m
解析试题分析: (1)设小球离开B点做平抛运动的时间为t1,落地点到C点距离为s
由h =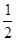 gt12
gt12
得: t1=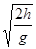 =
=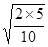 s =" 1" s
s =" 1" s
s = vB·t1 =" 2×1" m =" 2" m
(2)小球到达B受重力G和向上的弹力F作用,由牛顿第二定律知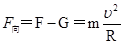
解得F=3N
由牛顿第三定律知球对B的压力F’="F" =3N 方向竖直向下。
(3)如图,斜面BEC的倾角θ=45°,CE长d =" h" = 5m,因为d> s,所以小球离开B点后能落在斜面上
假设小球第一次落在斜面上F点,BF长为L,小球从B点到F点的时间为t2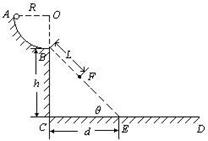
Lcosθ= vBt2 ①
Lsinθ=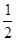 gt22 ②
gt22 ②
联立①、②两式得
t2 = 0.4s
L =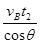 =
= m = 0.8
m = 0.8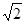 m = 1.13m
m = 1.13m
考点: 平抛运动;向心力

 一课一练课时达标系列答案
一课一练课时达标系列答案关于平抛运动,下面的几种说法正确的是( )
| A.平抛运动是一种不受任何外力作用的运动 |
| B.平抛运动是曲线运动,它的速度方向不断改变,不可能是匀变速运动 |
| C.平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动 |
| D.平抛运动的落地时间与初速度大小无关,而落地时的水平位移与抛出点的高度有关 |
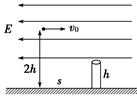
(1)平抛物体的运动规律可以概括为两点:①水平方向做匀速运动,②竖直方向做自由落体运动。为了研究平抛物体的运动,可做下面的实验:如图1所示,用小锤打击弹性金属片,A球就水平飞出,同时B球被松开,做自由落体运动,两球同时落到地面,这个实验能够说明( )
| A.只能说明上述规律中的第①条 |
| B.只能说明上述规律中的第②条 |
| C.不能说明上述规律中的任何一条 |
| D.能同时说明上述两条规律 |
 ,小球平抛运动初速度的计算式为
,小球平抛运动初速度的计算式为 (用L、g表示)。
(用L、g表示)。


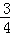 d,重力加速度为g.忽略手的运动半径和空气阻力,绳能承受的最大拉力为定值.
d,重力加速度为g.忽略手的运动半径和空气阻力,绳能承受的最大拉力为定值.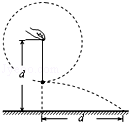
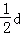 ,要使绳仍在球运动到最低点时恰好断掉,求小球飞行的水平距离.
,要使绳仍在球运动到最低点时恰好断掉,求小球飞行的水平距离.