题目内容
8. 如图所示,半径为R的光滑半圆环AB竖直固定在光滑水平地面上,质量为m的小球以某一速度v0从A点进入半圆环,恰好经最高点B水平向左飞出(不计空气阻力).求:
如图所示,半径为R的光滑半圆环AB竖直固定在光滑水平地面上,质量为m的小球以某一速度v0从A点进入半圆环,恰好经最高点B水平向左飞出(不计空气阻力).求:(1)小球在A点做圆周运动时,小球对轨道的压力大小;
(2)小球从B点飞出时的速度大小;
(3)小球从B点落到水平地面上的C点,水平位移AC的大小.
分析 (1)、(2)由题意,小球恰好能经过最高点B,此时由重力提供小球所需要的向心力,根据牛顿第二定律可求得小球在B点时的速度.从A到B过程,只有重力做功,小球的机械能守恒,即可列式求出小球通过A点时的速度大小.再根据牛顿运动定律求小球对轨道的压力大小.
(3)小球离开B点后做平抛运动,运用运动的分解法即可求得水平位移AC的大小.
解答 解:(1)、(2)因为小球刚好能通过最高点B,所以在最高点刚好又重力提供向心力,由牛顿二定律可得:
mg=m$\frac{{v}_{B}^{2}}{R}$
解得:vB=$\sqrt{gR}$
选取A点所在的水平面为零重力势能面,小球从A到B的过程中机械能守恒,则有:
$\frac{1}{2}m{v}_{A}^{2}$=$\frac{1}{2}m{v}_{B}^{2}$+2mgR
由①②式联立可得:vA=$\sqrt{5gR}$
在A点,由F-mg=m$\frac{{v}_{A}^{2}}{R}$得
F=6mg
根据牛顿第三定律知小球在A点做圆周运动时,小球对轨道的压力大小 F′=F=6mg
(3)小球做平抛过程的落地时间为t,则有:
2R=$\frac{1}{2}g{t}^{2}$
得:t=2$\sqrt{\frac{R}{g}}$
小球做平抛的水平位移:xAC=vBt…⑤
由①④⑤式可得:xAC=2R
答:
(1)小球在A点做圆周运动时,小球对轨道的压力大小是6mg;
(2)小球从B点飞出时的速度大小是$\sqrt{gR}$;
(3)小球从B点落到水平地面上的C点,水平位移AC的大小是2R.
点评 本题是向心力、机械能守恒和平抛运动的综合,掌握小球通过最高点的临界条件是解题的关键.同时要求我们要正确的对小球进行运动过程的分析和特定位置的受力分析.

| A. | 电动势表征电源把其它形式的能转变为电能的本领 | |
| B. | 照明电路中使用的电灯越多,电路的总电阻也越大,电源路端电压越高 | |
| C. | 外电路断开时的路端电压数值上等于电源电动势 | |
| D. | 外电路短路时的路端电压数值上趋近于电源的电动势 |
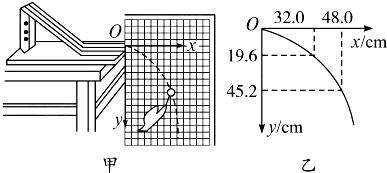
 甲、乙两小分队进行代号为“猎狐”的军事演习,指挥部通过现代通信设备,在荧屏上观察到两小分队的具体行军路线如图所示.两小分队同时同地由O点出发,最后同时捕“狐”于A点.下列说法正确的是( )
甲、乙两小分队进行代号为“猎狐”的军事演习,指挥部通过现代通信设备,在荧屏上观察到两小分队的具体行军路线如图所示.两小分队同时同地由O点出发,最后同时捕“狐”于A点.下列说法正确的是( )| A. | 小分队行军路程s甲>s乙 | B. | 小分队平均速度v甲>v乙 | ||
| C. | 小分队的平均速率相等 | D. | 图象表示的是位移-时间图象 |
 如图所示,有一直角V型槽,固定在水平地面上,槽的两侧壁与水平面的夹角均为45°.有一质量为m的立方体均匀木块放在槽内.木块与槽两侧面间的动摩擦因素分别为μ1和μ2,且μ1>μ2.现用水平力推木块使之沿槽方向运动,则木块所受摩擦力为( )
如图所示,有一直角V型槽,固定在水平地面上,槽的两侧壁与水平面的夹角均为45°.有一质量为m的立方体均匀木块放在槽内.木块与槽两侧面间的动摩擦因素分别为μ1和μ2,且μ1>μ2.现用水平力推木块使之沿槽方向运动,则木块所受摩擦力为( )| A. | $\frac{\sqrt{2}}{2}$(μ1+μ2)mg | B. | $\frac{\sqrt{2}}{4}$(μ1+μ2)mg | C. | $\frac{{μ}_{1}+{μ}_{2}}{2}$mg | D. | $\frac{\sqrt{2}}{2}$μ1mg |
| A. | M(g-$\frac{{V}^{2}}{R}$) | B. | M(g+$\frac{{V}^{2}}{R}$) | C. | M($\frac{{V}^{2}}{R}$-g) | D. | Mg |
| A. | 时间间隔 | B. | 位移 | C. | 路程 | D. | 速度 |

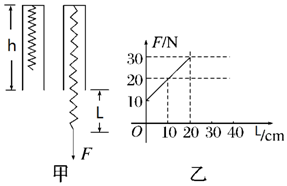 某同学在研究性学习中,利用所学的知识解决了如下问题:一轻弹簧竖直悬挂于某一深度为h=35.0cm,且开口向下的小筒中(没有外力作用时弹簧的下部分位于筒内,但测力计可以同弹簧的下端接触),如图甲所示,如果本实验的长度测量工具只能测量出筒的下端弹簧的长度l,现要测出弹簧的原长l0和弹簧的劲度系数k,该同学通过改变l而测出对应的弹力F,作出F-l变化的图线如图乙所示,则弹簧的劲度系数k=100N/m,弹簧的原长l0=25cm.
某同学在研究性学习中,利用所学的知识解决了如下问题:一轻弹簧竖直悬挂于某一深度为h=35.0cm,且开口向下的小筒中(没有外力作用时弹簧的下部分位于筒内,但测力计可以同弹簧的下端接触),如图甲所示,如果本实验的长度测量工具只能测量出筒的下端弹簧的长度l,现要测出弹簧的原长l0和弹簧的劲度系数k,该同学通过改变l而测出对应的弹力F,作出F-l变化的图线如图乙所示,则弹簧的劲度系数k=100N/m,弹簧的原长l0=25cm.