Question

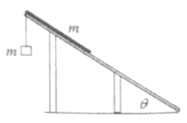
【题目】如图，倾角为θ的光滑斜面固定在地面上，长为l，质量为m、质量分布均匀的软绳置于斜面上，其上端与斜面顶端齐平。设斜面顶端为零势能面。用细线将质量也为m的小物块与软绳连接，物块由静止释放后向下运动，直到软绳刚好全部离开斜面（此时物块未到达地面）。软绳刚好离开斜面时，软绳的重力势能为_____，此时物块的速度大小为_____。

Answer 1

【答案】﹣mgl(1﹣sinθ)

【解析】

[1]物块未释放时，软绳的重心离斜面顶端的高度为：

h1=lsinθ

软绳刚好全部离开斜面时，软绳的重心离斜面顶端的高度：

h2=l

则软绳重力势能共减少：

mgl(1﹣sinθ)

设斜面顶端为零势能面，软绳重力势能为：

﹣mgl(1﹣sinθ)；

[2]根据能量转化和守恒定律：

mgl+mgl(1﹣sinθ)=

得：。