题目内容
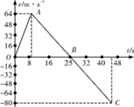
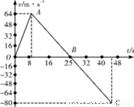
(12分)一宇宙空间探测器从某一星球表面垂直升空,假设探测器的质量恒为1500kg,发动机的推力为恒力,宇宙探测器升空到某一高度时,发动机突然关闭,如图为其速度随时间的变化规律,求:

⑴宇宙探测器在该行星表面能达到的最大高度;
⑵计算该行星表面的重力加速度;
⑶假设行星表面没有空气,试计算探测器的发动机工作时的推力大小。
【答案】
⑴Hm=768m;⑵g=4m/s2;⑶F=18000N
【解析】
试题分析:⑴在v-t图象中,图线与时间轴所围的面积表示了物体的位移,在时间轴的上方,面积为正,在时间轴的下方,面积为负,由v-t图象可知,宇宙探测器在该行星表面能达到的最大高度为:Hm= ×24×64m=768m
×24×64m=768m
⑵当关闭发动机后,探测器仅在行星对它的重力mg作用下做匀变速直线运动,在v-t图象中,图线的斜率表示了其运动的加速度,根据牛顿第二定律有:a2=-g= m/s2
m/s2
解得该行星表面的重力加速度为:g=4m/s2
⑶由图线OA段可知,发动机工作时探测器加速度为:a1= =8m/s2
=8m/s2
根据牛顿第二定律有:F-mg=ma1
解得探测器的发动机工作时的推力为:F=m(g+a1)=1500×(4+8)N=18000N
考点:本题主要考查了对v-t图象的理解及牛顿第二定律的应用问题,属于中档题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目