题目内容
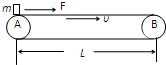
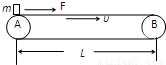
如图所示，传送带以恒定速度υ=3m/s向右运动，AB长L=3.8m，质量为m=5kg的物体，无初速地放到左端A处，同时用水平恒力F=25N向右拉物体，如物体与传送带间的动摩擦因数μ=0.25，求：物体从A到B所需时间．（重力加速度g=10m/s2）分析：木块的运动分为两个过程，刚开始摩擦力向右，木块匀加速运动，当木块的速度增加到等于皮带的传送速度后，物体在拉力作用下要进一步加速，故摩擦力变为向左，但小于拉力F，木块继续向右加速，直到离开皮带为止．
解答：解：刚开始将木块无初速地放到皮带左端A处，由于皮带向右运动，故木块受到向右的滑动摩擦力，木块还受到重力、支持力和拉力，根据牛顿第二定律，有
F+μmg=ma1
解得a1=
+μg=
+0.25×10=7.5m/s2
木块的速度增加到等于皮带传送速度的时间设为t，根据运动学公式，有
v=a1t1
x1=
代入数据解得
t1=0.4s
x1=0.6m
接下来，摩擦力变为向左，物体继续加速，直到掉下皮带为止
根据牛顿第二定律，有
F-μmg=ma2 ①
根据位移时间公式，有
L-x1=vt2+
at22 ②
由①②两式解得
a2=2.5m/s2
t2=0.8s
故总时间
t=t1+t2=1.2s
即物体从A到B所需时间为1.2s．
F+μmg=ma1
解得a1=
| F |
| m |
| 25 |
| 5 |
木块的速度增加到等于皮带传送速度的时间设为t，根据运动学公式，有
v=a1t1
x1=
| v2 |
| 2a1 |
代入数据解得
t1=0.4s
x1=0.6m
接下来，摩擦力变为向左，物体继续加速，直到掉下皮带为止
根据牛顿第二定律，有
F-μmg=ma2 ①
根据位移时间公式，有
L-x1=vt2+
| 1 |
| 2 |
由①②两式解得
a2=2.5m/s2
t2=0.8s
故总时间
t=t1+t2=1.2s
即物体从A到B所需时间为1.2s．
点评：本题关键将皮带上木块的运动分为两个加速度不等的匀加速运动过程进行分析．
练习册系列答案
口算题天天练系列答案
相关题目
如图所示，传送带足够长，正以2m/s的速度匀速传送，现将下表面涂有颜料的木块（可视为质点）轻放在传送带左端，已知木块与传送带间的动摩擦因素为0.05．求在下列情况下木块在传送带上留下的划痕：
如图所示，传送带以恒定速度υ=3m/s向右运动，AB长L=3.8m，质量为m=5kg的物体，无初速地放到左端A处，同时用水平恒力F=25N向右拉物体，如物体与传送带间的动摩擦因数μ=0.25，求：物体从A到B所需时间．（重力加速度g=10m/s2）
