题目内容
8. 如图所示,小木块在沿斜面向上的恒定外力F作用下,从A点由静止开始作匀加速运动,前进了0.45m抵达B点时,立即撤去外力.此后小木块又前进0.15m到达C点,速度为零.已知木块与斜面动摩擦因数μ=$\frac{\sqrt{3}}{6}$,木块质量m=1kg.(g=10m/s2)求:
如图所示,小木块在沿斜面向上的恒定外力F作用下,从A点由静止开始作匀加速运动,前进了0.45m抵达B点时,立即撤去外力.此后小木块又前进0.15m到达C点,速度为零.已知木块与斜面动摩擦因数μ=$\frac{\sqrt{3}}{6}$,木块质量m=1kg.(g=10m/s2)求:(1)木块向上经过B点时速度为多大?
(2)木块在AB段所受的外力F多大?
(3)撤去外力F后,木块返回A点时的速度多大?
分析 (1)对小滑块加速和减速过程分别受力分析,加速过程受推力、重力、支持力和摩擦力,减速过程,推力撤销,其余力不变;然后对两个过程运用牛顿第二定律求出加速度,再根据速度位移公式列式求解;
(2)依据第一问的解答,可以进一步得到外力F的大小;
(3)木块下降过程,先受力分析,受重力、支持力和摩擦力,根据牛顿第二定律求解加速度,再根据运动学公式求解木速度
解答 解:(1)小滑块加速过程受推力、重力、支持力和摩擦力,根据牛顿第二定律,有
F-mgsinθ-μmgcosθ=ma1 ①
小滑块减速过程受重力、支持力和摩擦力,根据牛顿第二定律,有
mgsinθ+μmgcosθ=ma2 ②
对于加速过程,根据运动学公式,有
${x}_{1}=\frac{{v}^{2}}{2{a}_{1}}$ ③
对于减速过程,根据运动学公式,同样有
${x}_{2}=\frac{{v}^{2}}{2{a}_{2}}$ ④
有①②③④解得
v=1.5 m/s
F=10 N
故木块向上经过B点时速度为1.5m/s;
(2)木块在AB段所受的外力F为10N;
(3)木块下降过程受重力、支持力和摩擦力,根据牛顿第二定律,有
mgsinθ-μmgcosθ=ma3 ⑤
根据速度位移公式,有
${v′}_{A}^{2}=2{a}_{3}({x}_{1}+{x}_{2})$ ⑥
解得
v′A=$\sqrt{3}$m/s
即木块回到A点的速度v为$\sqrt{3}$
答:(1)木块向上经过B点时速度为1.5m/s
(2)木块在AB段所受的外力F为10N
(3)撤去外力F后,木块返回A点时的速度为$\sqrt{3}m/s$
点评 本题关键是对木块受力分析,根据牛顿第二定律求出各个时间段的加速度,然后根据运动学公式列式求解

 今有某小型发电机和一理想变压器连接后给一个灯泡供电,电路如图(电压表和电流表均为理想电表).已知该发电机线圈匝数为N,电阻为r,当线圈以转速n匀速转动时,电压表示数为U,灯泡(额定电压为U.,电阻恒为R)恰能正常发光,则( )
今有某小型发电机和一理想变压器连接后给一个灯泡供电,电路如图(电压表和电流表均为理想电表).已知该发电机线圈匝数为N,电阻为r,当线圈以转速n匀速转动时,电压表示数为U,灯泡(额定电压为U.,电阻恒为R)恰能正常发光,则( )| A. | 变压器的匝数比为U0:U | |
| B. | 电流表的示数为$\frac{{{U}_{0}}^{2}}{RU}$ | |
| C. | 在图示位置时,发电机线圈的磁通量为$\frac{{\sqrt{2}U}}{2Nnπ}$ | |
| D. | 从图示位置开始计时,变压器输入电压的瞬时值表达式为u=Usin2nπt |
| A. | 物体的末速度一定等于初速度的5倍 | |
| B. | 物体的末速度一定比初速度大5m/s | |
| C. | 物体的初速度一定比前1s内的末速度大5m/s | |
| D. | 物体的末速度一定比前1s内的初速度大5m/s |
 如图所示的实验中,平行板电容器的极板A与静电计小球连接,极板B和静电计外壳都接地.若极板B稍向上移一些,则( )
如图所示的实验中,平行板电容器的极板A与静电计小球连接,极板B和静电计外壳都接地.若极板B稍向上移一些,则( )| A. | 电容器电容变大,静电计指针偏角不变 | |
| B. | 电容器电容变小,静电计指针偏角变小 | |
| C. | 极板上的电量不变,静电计指针偏角变大 | |
| D. | 极板上的电量不变,静电计指针偏角变小 |
| A. | 电视机后盖上开有许多小孔 | B. | 静电除尘 | ||
| C. | 静电喷涂 | D. | 静电复印 |
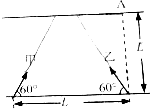 如图,河的宽度为L′,河水流速为μ,甲、乙两船均以静水中的速度v同时渡河,出发时两船相距L,甲、乙船头均与岸边成60°角,且乙船恰好能直达正对岸的A点.则下列判断正确的是( )
如图,河的宽度为L′,河水流速为μ,甲、乙两船均以静水中的速度v同时渡河,出发时两船相距L,甲、乙船头均与岸边成60°角,且乙船恰好能直达正对岸的A点.则下列判断正确的是( )| A. | 甲船正好也在A点靠岸 | B. | 甲船在A点左侧靠岸 | ||
| C. | v:u=2:$\sqrt{3}$ | D. | 甲乙两船到达对岸的时间相等 |
 一匀强磁场分布在以O为圆心,半径为R的圆形区域内,方向与纸面垂直,如图所示,质量为m、电荷量q的带正电的质点,经电场加速后,以速度v沿半径MO方向进入磁场,沿圆弧运动到N点,然后离开磁场,∠MON=120°,质点所受重力不计,求:
一匀强磁场分布在以O为圆心,半径为R的圆形区域内,方向与纸面垂直,如图所示,质量为m、电荷量q的带正电的质点,经电场加速后,以速度v沿半径MO方向进入磁场,沿圆弧运动到N点,然后离开磁场,∠MON=120°,质点所受重力不计,求: 如图所示,长s=5m、倾角θ=37°的斜面各通过一小段光滑圆弧与水平传送带和水平地面平滑连接,传送带长L=1.6m,以恒定速率v0=4m/s逆时针运行,将一可看作质点的物块轻轻地放上传送带右端A,物块滑到传送带左端B时恰好与传送带共速并沿斜面下滑,已知物块和传送带、斜面、水平地面间的动摩擦因数都为μ,物块最终静止在水平面上的D点,取g=10m/s2,求:
如图所示,长s=5m、倾角θ=37°的斜面各通过一小段光滑圆弧与水平传送带和水平地面平滑连接,传送带长L=1.6m,以恒定速率v0=4m/s逆时针运行,将一可看作质点的物块轻轻地放上传送带右端A,物块滑到传送带左端B时恰好与传送带共速并沿斜面下滑,已知物块和传送带、斜面、水平地面间的动摩擦因数都为μ,物块最终静止在水平面上的D点,取g=10m/s2,求: