题目内容
 如图所示,一质量为m的带电小球,用长为L的绝缘细线悬挂在水平向右,场强为E的匀强电场中,静止时悬线与竖直方向成θ角(θ<45°)
如图所示,一质量为m的带电小球,用长为L的绝缘细线悬挂在水平向右,场强为E的匀强电场中,静止时悬线与竖直方向成θ角(θ<45°)(1)求小球带何种电性及所带电荷量大小;
(2)如果不改变电场强度的大小而突然将电场的方向变为竖直向下,带电小球将怎样运动?带电小球的最大速度值是多少?
分析:(1)电场力向左,故电荷带负电;根据平衡条件求解电场力,然后求解电荷量;
(2)电场力变为竖直后,小球做摆动,根据动能定理列式求解最大速度.
(2)电场力变为竖直后,小球做摆动,根据动能定理列式求解最大速度.
解答:解:(1)小球带负电,带电小球处于平衡状态,有:
qE-mgtanθ=0 ①
解得:q=
②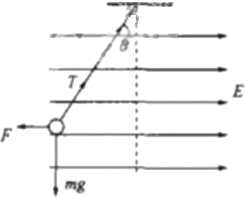
(2)小球在竖直平面内沿圆弧摆下,做圆周运动.(或沿圆弧摆下然后沿圆弧来回运动)带电小球到最低点时速度最大,设小球的最大速度为vm,小球摆下过程中重力做正功,电场力做负功,由动能定理得:
mgl(1-cosθ)-qEl(1-cosθ)=
m
③
联立①③式得:vm=
答:(1)小球带负电性,所带电荷量大小为
;
(2)如果不改变电场强度的大小而突然将电场的方向变为竖直向下,带电小球将沿圆弧来回运动,带电小球的最大速度值是
.
qE-mgtanθ=0 ①
解得:q=
| mgtanθ |
| E |

(2)小球在竖直平面内沿圆弧摆下,做圆周运动.(或沿圆弧摆下然后沿圆弧来回运动)带电小球到最低点时速度最大,设小球的最大速度为vm,小球摆下过程中重力做正功,电场力做负功,由动能定理得:
mgl(1-cosθ)-qEl(1-cosθ)=
| 1 |
| 2 |
| v | 2 m |
联立①③式得:vm=
| 2gl(1-cosθ)(1-tanθ) |
答:(1)小球带负电性,所带电荷量大小为
| mgtanθ |
| E |
(2)如果不改变电场强度的大小而突然将电场的方向变为竖直向下,带电小球将沿圆弧来回运动,带电小球的最大速度值是
| 2gl(1-cosθ)(1-tanθ) |
点评:本题关键是对小球受力分析后根据平衡条件和动能定理列式求解,不难.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,一质量为m,带电荷量为+q的小物体,在水平方向的匀强磁场B中,从倾角为
如图所示,一质量为m,带电荷量为+q的小物体,在水平方向的匀强磁场B中,从倾角为 如图所示,一质量为m=0.016kg、长L=0.5m、宽d=0.1m、电阻R=0.1Ω的矩形线圈,从h1=5m的高处由静止开始下落,然后进入高度为h2(h2>L)的匀强磁场.下边刚进入磁场时,线圈正好作匀速运动.线圈的下边通过磁场所经历的时间t=0.15s.取g=10m/s2
如图所示,一质量为m=0.016kg、长L=0.5m、宽d=0.1m、电阻R=0.1Ω的矩形线圈,从h1=5m的高处由静止开始下落,然后进入高度为h2(h2>L)的匀强磁场.下边刚进入磁场时,线圈正好作匀速运动.线圈的下边通过磁场所经历的时间t=0.15s.取g=10m/s2 如图所示,一质量为m的物块恰好沿着倾角为θ的斜面匀速下滑.现对物块施加一个竖直向下的恒力F.则物块( )
如图所示,一质量为m的物块恰好沿着倾角为θ的斜面匀速下滑.现对物块施加一个竖直向下的恒力F.则物块( ) 如图所示,一质量为m的小球,用长为l的轻绳悬挂于O点,小球在水平恒力F的作用下,从最低点A点拉至B点的过程中,力F所做的功为( )
如图所示,一质量为m的小球,用长为l的轻绳悬挂于O点,小球在水平恒力F的作用下,从最低点A点拉至B点的过程中,力F所做的功为( ) 如图所示,一质量为m=1.0×10-2kg,带电量为q=1.0×10-6C的小球,用绝缘细线悬挂在水平向右的匀强电场中,假设电场足够大,静止时悬线向左与竖直方向成37°角.小球在运动过程电量保持不变,重力加速度g取10m/s2.
如图所示,一质量为m=1.0×10-2kg,带电量为q=1.0×10-6C的小球,用绝缘细线悬挂在水平向右的匀强电场中,假设电场足够大,静止时悬线向左与竖直方向成37°角.小球在运动过程电量保持不变,重力加速度g取10m/s2.