题目内容
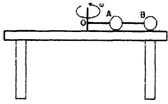 如图所示,A、B两个小球用轻质细杆连着,在光滑的水平桌面上以相同的角速度绕轴O做匀速圆周运动.两个小球的质量比mA:mB=1:2,OA:AB=1:1,则球的向心加速度之比aA:aB=
如图所示,A、B两个小球用轻质细杆连着,在光滑的水平桌面上以相同的角速度绕轴O做匀速圆周运动.两个小球的质量比mA:mB=1:2,OA:AB=1:1,则球的向心加速度之比aA:aB=1:2
1:2
;两段杆OA、AB受的拉力之比为5:4
5:4
.分析:A、B两球绕O点在光滑的水平面上以相同的角速度做匀速圆周运动,根据an=ω2r比较角速度;B球靠AB杆的拉力提供向心力,A球靠OB杆和AB杆的拉力的合力提供向心力,根据牛顿第二定律求出两段杆子的拉力之比.
解答:解:A、B两球绕O点在光滑的水平面上以相同的角速度做匀速圆周运动,根据公式an=ω2r,球的向心加速度之比aA:aB=1:2;
对B球有:TAB=2m?2l?ω2.
对A球有:TOA-TAB=mlω2.
联立两式解得:TOA:TAB=5:4;
故答案为:1:2,5:4.
对B球有:TAB=2m?2l?ω2.
对A球有:TOA-TAB=mlω2.
联立两式解得:TOA:TAB=5:4;
故答案为:1:2,5:4.
点评:解决本题的关键搞清向心力的来源,选择恰当的向心力公式并运用牛顿第二定律进行求解.

练习册系列答案
相关题目
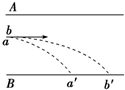 如图所示,a、b两个带正电的粒子,以相同的速度先后垂直于电场线从同一点进入平行板间的匀强电场后,a粒子打在B板的a′点,b粒子打在B板的b′点,若不计重力,则( )
如图所示,a、b两个带正电的粒子,以相同的速度先后垂直于电场线从同一点进入平行板间的匀强电场后,a粒子打在B板的a′点,b粒子打在B板的b′点,若不计重力,则( )| A、a的电荷量一定大于b的电荷量 | B、b的质量一定大于a的质量 | C、a的比荷一定大于b的比荷 | D、b的比荷一定大于a的比荷 |

 如图所示,A、B两个物块的重力分别是GA=3N,GB=4N,弹簧的重力不计,整个装置沿竖直方向处于静止状态,这时弹簧的弹力F=2N,则天花板受到的拉力和地板受到的压力,有可能是( )
如图所示,A、B两个物块的重力分别是GA=3N,GB=4N,弹簧的重力不计,整个装置沿竖直方向处于静止状态,这时弹簧的弹力F=2N,则天花板受到的拉力和地板受到的压力,有可能是( ) 如图所示,A、B两个物体间用最大张力为100N的轻绳相连,mA=4kg,mB=8kg,在拉力F的作用下向上加速运动,为使轻绳不被拉断,F的最大值是多少?(g取10m/s2)
如图所示,A、B两个物体间用最大张力为100N的轻绳相连,mA=4kg,mB=8kg,在拉力F的作用下向上加速运动,为使轻绳不被拉断,F的最大值是多少?(g取10m/s2)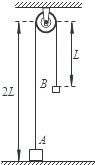 如图所示,A、B两个小物体(可看成质点)的质量分别为2m、m,它们栓接在跨过定滑轮的细绳两端,细绳不可伸长,且能承受足够大的拉力.B物体悬吊着静止时,A也静止在地面上,A、B与定滑轮轮轴之间的竖直距离分别为2L、L.现将B物体竖直向上提高距离l,再将其从静止释放.每次细绳被拉直时A、B速度的大小立即变成相等,且速度方向相反,由于细绳被拉直的时间极短,此过程中重力的作用可以忽略不计.物体与地面接触时,速度立即变为0,直到再次被细绳拉起.细绳始终在滑轮上,且不计一切摩擦.重力加速度为g.求
如图所示,A、B两个小物体(可看成质点)的质量分别为2m、m,它们栓接在跨过定滑轮的细绳两端,细绳不可伸长,且能承受足够大的拉力.B物体悬吊着静止时,A也静止在地面上,A、B与定滑轮轮轴之间的竖直距离分别为2L、L.现将B物体竖直向上提高距离l,再将其从静止释放.每次细绳被拉直时A、B速度的大小立即变成相等,且速度方向相反,由于细绳被拉直的时间极短,此过程中重力的作用可以忽略不计.物体与地面接触时,速度立即变为0,直到再次被细绳拉起.细绳始终在滑轮上,且不计一切摩擦.重力加速度为g.求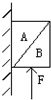 如图所示,A、B两个物体被一个竖直向上力F托着,处于静止状态,则A物体一共受
如图所示,A、B两个物体被一个竖直向上力F托着,处于静止状态,则A物体一共受