题目内容
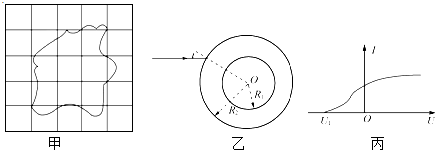
如图甲所示，高h、长Ｌ的光滑绝缘正方形台面上加有一竖直向下、磁感应强度B的匀强磁场．在台面右侧接着一个与内侧边线对齐、每板宽为d（d＜
）的平行板电容器（电容器有光滑绝缘的底部），右板接电源的正极，左板接电源负极，现有质量为m、电量为+q的一群粒子（视为质点）从靠近右板在底部由静止释放，通过左板的小孔进入磁场，不计一切阻力，重力加速度取g．求：
(1)若取电容器的电压为U，求这些带电粒子在磁场中运动的半径；
(2)若要求这些粒子都从台面右侧射出，则电容器的电压应满足什么条件？
(3)在地面上建立如图坐标系，当
时，在图乙中画出这些粒子落地时在这个坐标系中
的痕迹（要求写出计算说明的过程并大致标明痕迹的位置）。
 |
解：（1）在电容器中，根据动能定理，有：
①(2分)
在磁场中，根据洛牛顿第二定律，有：
②(2分)
①②联立得粒子运动的半径为：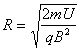
③(2分)
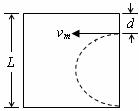
(2)当在电容器底部外侧经加速的粒子恰好能从台面的外侧相切射出时，粒子的半径最大，如图所示．
即
④(2分)
④代入③解得：
⑤(1分)
当U＞0，在电容器内侧粒子，那怕不能一次在磁场中从台面右侧射出，也可以再进入电容器减速至底部右侧，又再重新加速进入磁场，多周后也能从台面右侧射出。(2分)
故电容器的电压满足的条件为：
。 (1分)
(3)把代入③得粒子运动的半径为：
(1分)
说明当粒子从电容器远侧射入磁场时，粒子从台面右侧中点射出，当粒子从电容器近侧射入磁场时，粒子从台面距中点为d处射出。 (1分)
粒子从台面右侧射出后做平抛运动，设它的落地时间为t。
由
，得：
(1分)
粒子水平位移
(1分) ks5u
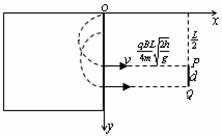
至此可作得这些粒子落地时的轨迹如下图所示中的PQ连线。（2分）
如图甲所示，高h、长L的光滑绝缘正方形台面上加有一竖直向下、磁感应强度B的匀强磁场．在台面右侧接着一个与内侧边线对齐、每板宽为d（d＜
）的平行板电容器（电容器有光滑绝缘的底部），右板接电源的正极，左板接电源负极，现有质量为m、电量为+q的一群粒子（视为质点）从靠近右板在底部由静止释放，通过左板的小孔进入磁场，不计一切阻力，重力加速度取g．求：
时，在图乙中画出这些粒子落地时在这个坐标系中