Question

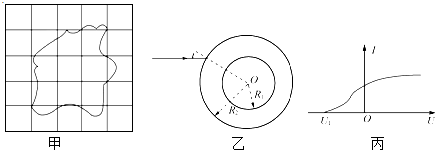
如图甲所示，高h、长L的光滑绝缘正方形台面上加有一竖直向下、磁感应强度B的匀强磁场．在台面右侧接着一个与内侧边线对齐、每板宽为d（d＜

L

2

）的平行板电容器（电容器有光滑绝缘的底部），右板接电源的正极，左板接电源负极，现有质量为m、电量为+q的一群粒子（视为质点）从靠近右板在底部由静止释放，通过左板的小孔进入磁场，不计一切阻力，重力加速度取g．求：
（1）若取电容器的电压为U，求这些带电粒子在磁场中运动的半径；
（2）若要求这些粒子都从台面右侧射出，则电容器的电压应满足什么条件？
（3）在地面上建立如图坐标系，当U=

qB 2L 2

32m

时，在图乙中画出这些粒子落地时在这个坐标系中
的痕迹（要求写出计算说明的过程并大致标明痕迹的位置）．

Answer 1

分析：（1）由动能定理可求得带电粒子离开电容器时的速度，再由洛仑力充当向心力可求得粒子在磁场中的半径；
（2）由几何关系可得出最大半径，则可求出最大电压，分析粒子的运动可得出电压的范围；
（3）由已知电压可得出粒子在磁场中的半径，分析粒子到这位置，再根据电场中的类平抛运动规律可求得粒了偏转的位移．

解答：解：（1）在电容器中，根据动能定理可知qU=

1

2

mv² ①
在磁场中，根据洛仑兹力充当向心力可知：
BqV=m

v2

R

  ②
联立解得粒子的运动半径为：R=

2mU qB2

    ③

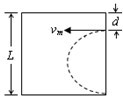
（2）当在电容器底部外侧经加速的粒子恰好能从台面的外侧相切射出时，粒子的半径最大，如图所示：
即：R_m=

L-d

2

解得：U_m=

(L-d)2qB2

8m

；
当U＞0时，在电容器内侧粒子，那怕不能一次在磁场中从台面右侧射出，也可以再进入电容器减速至底部右侧，又再重新加速进入磁场，多周后也能从台面右侧射出．
故电容器的电压满足的条件为：0＜U_m≤

(L-d)2qB2

8m

；
（3）把U=

qB2L2

32m

代入③得粒子运动半径为R=

L

4

；
说明当粒子从电容器远侧射入磁场时，粒子从台面右侧中点射出，当粒子从电容器近侧射入磁场时，粒子从台面距中点为d处射出．
粒子从台面右侧射出后做平抛运动，设它的落地时间为t．
由h=

1

2

gt²，得t=

2h g

粒子水平位移x=vt=

qmL

4m

2h g

可作出这些粒子落地时的轨迹如下图所示的PQ曲线；

答：（1）粒子的运动半径为：R=

2mU qB2

；（2）电容器的电压满足的条件为：0＜U_m≤

(L-d)2qB2

8m

；（3）如图中PQ．

点评：本题为带电粒子磁场及电场中的运动问题，要注意全面掌握粒子的运动情况，明确几何关系及运动的合成与分解在解题中的应用．