题目内容
 质量为50kg的运动员,在一座高桥上做“蹦极”运动.他所用的弹性绳自由长度L=12m,假设弹性绳中的弹力与弹性绳的伸长之间的关系遵循胡克定律,弹性绳的弹性势能公式为Ek=
质量为50kg的运动员,在一座高桥上做“蹦极”运动.他所用的弹性绳自由长度L=12m,假设弹性绳中的弹力与弹性绳的伸长之间的关系遵循胡克定律,弹性绳的弹性势能公式为Ek=| 1 | 2 |
(1)运动员到达C点时的加速度;
(2)弹性绳的劲度系数;
(3)运动员到达C点时,运动员的速度大小.
分析:(1)在C点速度最大,则C点是平衡位置,则有重力等于弹力,加速度为零.
(2)由图读出C点下落的距离,结合胡克定律即可求解劲度系数k;
(3)对由O到C的过程运用机械能守恒定律列式即可求解;
(2)由图读出C点下落的距离,结合胡克定律即可求解劲度系数k;
(3)对由O到C的过程运用机械能守恒定律列式即可求解;
解答:解:(1)由图知,C点速度最大,C点是平衡位置,重力与弹力二力平衡,加速度为零.
(2)C点:mg=kx,
由图知s=20m,L=12m,则弹簧伸长的长度x=s-L=8m
则得 k=
=
=62.5 N/m;
(3)对由O到C的过程运用机械能守恒定律
mgs=
m
+
kx2
则得vC=
代入解得vC=8
m/s
答:(1)运动员到达C点时的加速度是0;
(2)弹性绳的劲度系数是62.5 N/m;
(3)运动员到达C点时,运动员的速度大小为8
m/s.
(2)C点:mg=kx,
由图知s=20m,L=12m,则弹簧伸长的长度x=s-L=8m
则得 k=
| mg |
| x |
| 50×10 |
| 8 |
(3)对由O到C的过程运用机械能守恒定律
mgs=
| 1 |
| 2 |
| v | 2 C |
| 1 |
| 2 |
则得vC=
|
代入解得vC=8
| 5 |
答:(1)运动员到达C点时的加速度是0;
(2)弹性绳的劲度系数是62.5 N/m;
(3)运动员到达C点时,运动员的速度大小为8
| 5 |
点评:本题首先读出图象的信息,分析运动员的运动情况.再选择平衡条件、机械能守恒定律等等物理规律求解.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
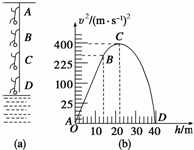 一质量为50kg的男孩在距离河流40m高的桥上做“蹦极跳”,原长AB为14m的弹性绳一端缚着他的双脚,另一端则固定在桥上的A点,如图(a)所示,然后男孩从桥面下坠直至贴近水面的最低点D.男孩的速率v跟下坠的距离h的变化关系如图(b)所示.假定绳在整个运动过程中遵守胡克定律,不考虑空气阻力、男孩的大小和绳的质量,g取10m/s2.
一质量为50kg的男孩在距离河流40m高的桥上做“蹦极跳”,原长AB为14m的弹性绳一端缚着他的双脚,另一端则固定在桥上的A点,如图(a)所示,然后男孩从桥面下坠直至贴近水面的最低点D.男孩的速率v跟下坠的距离h的变化关系如图(b)所示.假定绳在整个运动过程中遵守胡克定律,不考虑空气阻力、男孩的大小和绳的质量,g取10m/s2.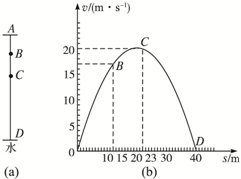 质量为50kg的男孩在距离河面40m高的桥上做“蹦极跳”,未拉伸前长度AB为15m的弹性绳一端缚着他的双脚,另一端则固定在桥上的A点,如图(a)所示,男孩从桥面下坠,达到的最低点为水面上方的一点D,假定绳在整个运动中遵守胡克定律.不计空气阻力、男孩的大小和绳的重力(g取10m/s2).男孩的速率v跟下坠的距离s的变化如图(b)所示,男孩在C点时速度最大.问:
质量为50kg的男孩在距离河面40m高的桥上做“蹦极跳”,未拉伸前长度AB为15m的弹性绳一端缚着他的双脚,另一端则固定在桥上的A点,如图(a)所示,男孩从桥面下坠,达到的最低点为水面上方的一点D,假定绳在整个运动中遵守胡克定律.不计空气阻力、男孩的大小和绳的重力(g取10m/s2).男孩的速率v跟下坠的距离s的变化如图(b)所示,男孩在C点时速度最大.问: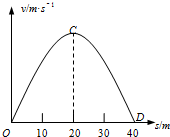 (2007?连云港三模)质量为50kg的小明,在一座高桥上做“蹦极”运动.他所用的轻弹性绳原长为12m,弹性绳中的弹力与弹性绳的伸长量遵循胡克定律,在整个运动中弹性绳不超过弹性限度.小明从桥面下落,能达到距桥面为40m的最低点D处,下落速率v跟下落距离s的关系如图所示,小明在C点时的速度最大.空气阻力不计,重力加速度g取10m/s2.(提示:弹力做功W=
(2007?连云港三模)质量为50kg的小明,在一座高桥上做“蹦极”运动.他所用的轻弹性绳原长为12m,弹性绳中的弹力与弹性绳的伸长量遵循胡克定律,在整个运动中弹性绳不超过弹性限度.小明从桥面下落,能达到距桥面为40m的最低点D处,下落速率v跟下落距离s的关系如图所示,小明在C点时的速度最大.空气阻力不计,重力加速度g取10m/s2.(提示:弹力做功W=