题目内容
4．一质点绕半径是R的圆周运动了$\frac{1}{4}$周，则路程为$\frac{1}{2}πR$，位移大小为$\sqrt{2}R$．分析 位移是由初位置指向末位置，是矢量；路程是运动轨迹的长度，是标量．
解答 解：质点只运动了$\frac{1}{4}$周，则路程是$\frac{1}{4}$个周长，为$\frac{1}{2}πR$．位移由初位置指向末位置，连接初末位置，根据勾股定理，位移的大小为$\sqrt{2}R$．
故答案为：$\frac{1}{2}πR$，$\sqrt{2}R$．
点评 解决本题的关键掌握位移和路程的区别：位移是由初位置指向末位置，是矢量；路程是运动轨迹的长度，是标量．
练习册系列答案
相关题目
在如图所示，两条虚线之间区域内存在沿y轴负方向的匀强电场，场强大小为E，坐标系第四象限有一边长为$\sqrt{2}$L的绝缘正方形盒CDFG（内壁光滑），其内部存在垂直于纸面向外的匀强磁场（大小未知），且C、D两点恰好在x、y轴上，CD连线与x轴正方向成45°角．一质量为m，带电量为+q（重力不计）的带电粒子，从M板中心静止释放经MN两极板间的电场加速后，从N板中心孔S沿x轴正方向射入虚线区域内的电场中，经该电场偏转后垂直于CD从CD中点J处的小孔射入方盒内，已知粒子与盒壁碰撞过程中无动能和电荷损失．（所有结果只能用E、L、m、q表示）求：
12．关于位移和路程，下列说法正确的是（ ）
| A． | 物体沿直线向某一方向运动，通过的路程就是位移 | |
| B． | 物体沿直线向某一方向运动，通过的路程等于位移的大小 | |
| C． | 物体通过一段路程，其位移可能是零 | |
| D． | 物体通过的路程不等，但位移可能相同，反之两物体通过的位移不同时，路程可能相同 |
19．下面几个速度中属于瞬时速度的是（ ）
| A． | 汽车从甲站行驶到乙站的速度是60 km/h | |
| B． | 子弹出枪口的速度是620 m/s | |
| C． | 小球第5 s末的速度是6 m/s | |
| D． | 汽车通过某一站牌时的速度是72 km/h |
9．下列说法中正确的是（ ）
| A． | 只有体积很小的物体才可以当作质点 | |
| B． | “地球围绕太阳转”，是以地球为参考系 | |
| C． | “第3秒初”就是第2秒末，指的是时刻 | |
| D． | 位移的大小和路程总是相等的，但位移是矢量，路程是标量 |
14．
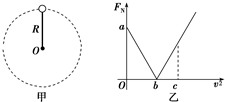如图甲所示，一轻杆一端固定在O点，另一端固定一小球，在竖直平面内做半径为R的圆周运动．小球运动到最高点时，杆与小球间弹力大小为FN，小球在最高点的速度大小为v，FN-v2图象如图乙所示．下列说法正确的是（ ）
如图甲所示，一轻杆一端固定在O点，另一端固定一小球，在竖直平面内做半径为R的圆周运动．小球运动到最高点时，杆与小球间弹力大小为FN，小球在最高点的速度大小为v，FN-v2图象如图乙所示．下列说法正确的是（ ）| A． | 当地的重力加速度大小为$\frac{b}{R}$ | B． | 小球的质量为$\frac{a}{b}R$ | ||
| C． | 当v2=c时，杆对小球弹力方向向上 | D． | 若v2=2b，则杆对小球弹力大小为a |