题目内容
质量为100kg的“勇气”号火星车于2004年成功登陆在火星表面.若“勇气”号在离火星表面12m时与降落伞自动脱离,此时“勇气”号的速度为4
m/s.被气囊包裹的“勇气”号第一次下落到地面后又弹跳到18m高处,这样上下碰撞了若干次后,才静止在火星表面上.已知火星的半径为地球半径的0.5倍,质量为地球质量的0.1倍.若“勇气”号第一次碰撞火星地面时,气囊和地面的接触时间为0.7s.求(地球表面的重力加速度g=10m/s2,不考虑火星表面空气阻力)
(1)“勇气”号第一次碰撞火星地面前的速度v1;
(2)“勇气”号和气囊第一次与火星碰撞时所受到的平均冲力F.
| 10 |
(1)“勇气”号第一次碰撞火星地面前的速度v1;
(2)“勇气”号和气囊第一次与火星碰撞时所受到的平均冲力F.
分析:(1)“勇气”号第一次碰撞火星地面前只受重力,机械能守恒,根据守恒定律列式求解;
(2)先根据机械能守恒定律求解出碰撞前后的速度,然后根据动量定理列式求解.
(2)先根据机械能守恒定律求解出碰撞前后的速度,然后根据动量定理列式求解.
解答:解:(1)设火星表面的重力加速度为g',地球表面的重力加速度为g
由万有引力定律有:
=mg
可得:
=
=
故:g′=
g=4m/s2
设探测器落地的速度为v1,则有:
mv02+mg′h1=
mv12
代入数据,解得:v1=16m/s
(2)反弹后,机械能守恒,有mg′h2=
mv22
解得v2=12m/s
设“勇气”号和气囊第一次与火星碰撞时所受到的平均冲力为F,
由动量定理得:
(F-mg′)t=m[v2-(-v1)]
代入数据,解得:N=4400N
答:(1)“勇气”号第一次碰撞火星地面前的速度为16m/s;
(2)“勇气”号和气囊第一次与火星碰撞时所受到的平均冲力为4400N.
由万有引力定律有:
| GMm |
| R2 |
可得:
| g′ |
| g |
M火
| ||
M地
|
| 2 |
| 5 |
故:g′=
| 2 |
| 5 |
设探测器落地的速度为v1,则有:
| 1 |
| 2 |
| 1 |
| 2 |
代入数据,解得:v1=16m/s
(2)反弹后,机械能守恒,有mg′h2=
| 1 |
| 2 |
解得v2=12m/s
设“勇气”号和气囊第一次与火星碰撞时所受到的平均冲力为F,
由动量定理得:
(F-mg′)t=m[v2-(-v1)]
代入数据,解得:N=4400N
答:(1)“勇气”号第一次碰撞火星地面前的速度为16m/s;
(2)“勇气”号和气囊第一次与火星碰撞时所受到的平均冲力为4400N.
点评:本题关键先求解出火星表面的重力加速度,然后根据机械能守恒定律和动量定理联立求解,不难.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
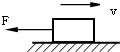 如图,质量为100kg的物在水平面上向右滑行,物体与水平面间的动摩擦因数μ为0.2,物体还受到一个向左的拉力F=4N,求:
如图,质量为100kg的物在水平面上向右滑行,物体与水平面间的动摩擦因数μ为0.2,物体还受到一个向左的拉力F=4N,求: 如图是一提升重物用的直流电动机工作时的电路图,电动机内阻为0.5Ω,R=10Ω,直流电压U=150V,理想电压表示数为100V,则( )
如图是一提升重物用的直流电动机工作时的电路图,电动机内阻为0.5Ω,R=10Ω,直流电压U=150V,理想电压表示数为100V,则( )