题目内容
9.一长为5m的长木板静止在光滑水平面上,某时刻一小铁块以速度7m/s从木板的右端滑上木板,此后长木板做匀加速直线运动,小铁块做匀减速直线运动,当长木板运动1.2米后二者速度恰好相等,此时小铁块距离长木板左端3m,求:(1)二者运动多长时间后速度相等;
(2)长木板和小铁块的加速度大小分别是多少?
分析 (1)小铁块从木板的右端滑上木板后,长木板做匀加速直线运动,小铁块做匀减速直线运动,已知速度相等时长木板的位移,由位移等于平均速度乘以时间列式.根据二者相对位移为2m列式,即可求时间.
(2)结合上题的结果,由加速度的定义式求解.
解答 解:(1)设二者运动t时向后速度相等,共同速度为v.
据题有:x板=$\frac{v}{2}t$=1.2m ①
二者相对位移大小为△x=5m-3m=2m
由△x=x铁-x板=$\frac{{v}_{0}+v}{2}t$-$\frac{v}{2}t$=$\frac{{v}_{0}}{2}t$ ②
解得 t=$\frac{2△x}{{v}_{0}}$=$\frac{2×2}{7}$s=$\frac{4}{7}$s
(2)由①得:v=$\frac{2{x}_{板}}{t}$=$\frac{2×1.2}{\frac{4}{7}}$=0.42m/s
根据牛顿第二定律得
长木板的加速度大小为 a板=$\frac{v-0}{t}$=$\frac{0.42}{\frac{4}{7}}$=0.735m/s2;
小铁块的加速度大小 a铁=$\frac{v-{v}_{0}}{t}$=$\frac{0.42-7}{\frac{4}{7}}$=-11.515m/s2.
答:
(1)二者运动$\frac{4}{7}$s时间后速度相等;
(2)长木板和小铁块的加速度大小分别是0.735m/s2和-11.515m/s2.
点评 该题涉及到相对运动的过程,要认真分析物体的受力情况和运动情况,并能熟练地运用匀变速直线运动的公式,明确相对位移等于两个物体位移之差,由牛顿第二定律和运动学公式结合解答.

练习册系列答案
相关题目
19.如图为一质点运动的位移时间图象,对其运动情况说法正确的是( )


| A. | 质点做曲线运动 | B. | 质点做直线运动 | ||
| C. | 质点的速度越来越大 | D. | 质点的速度越来越小 |
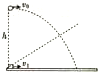 如图所示,一水平长木板的左端有一滑块,滑块正上方向高h=0.8m处有一小球,当滑块在长木板上以初速度v1=3m/s向右滑出的同时,小球以初速度v0=2m/s向右抛出,结果小球与滑块刚好能相遇,g=10m/s2,不计空气阻力,求:
如图所示,一水平长木板的左端有一滑块,滑块正上方向高h=0.8m处有一小球,当滑块在长木板上以初速度v1=3m/s向右滑出的同时,小球以初速度v0=2m/s向右抛出,结果小球与滑块刚好能相遇,g=10m/s2,不计空气阻力,求:
 如图所示,P是一个放射源,从开口处在纸面内向各个方向放出某种粒子(不计重力),而这些粒子最终必须全部垂直射到底片MN这一有效区域,并要求底片MN上每一地方都有粒子到达.假若放射源所放出的是质量为m、电量为q的带正电的粒子,且所有的粒子速率都是v,M与放射源的出口在同一水平面,底片MN竖直放置,底片MN长为L.为了实现上述目的,我们必须在P的出口处放置一有界匀强磁场.则匀强磁场的方向为垂直于纸面向外,匀强磁场的磁感应强度B的大小为$\frac{2mv}{qL}$,最小有界匀强磁场的面积S为$\frac{1}{4}$πL2.
如图所示,P是一个放射源,从开口处在纸面内向各个方向放出某种粒子(不计重力),而这些粒子最终必须全部垂直射到底片MN这一有效区域,并要求底片MN上每一地方都有粒子到达.假若放射源所放出的是质量为m、电量为q的带正电的粒子,且所有的粒子速率都是v,M与放射源的出口在同一水平面,底片MN竖直放置,底片MN长为L.为了实现上述目的,我们必须在P的出口处放置一有界匀强磁场.则匀强磁场的方向为垂直于纸面向外,匀强磁场的磁感应强度B的大小为$\frac{2mv}{qL}$,最小有界匀强磁场的面积S为$\frac{1}{4}$πL2.
 如图所示,A、B都是重物,A被绕过小滑轮P的细线悬挂,B放在粗糙的水平桌面上,滑轮P被一根斜短线系于天花板上的O点,O′是三根细线的结点,细线bO′水平拉着物体B,cO′沿竖直方向拉着弹簧.弹簧、细线、小滑轮的重力不计,细线与滑轮之间的摩擦力可忽略,整个装置处于静止状态.若重物A的质量为2kg,弹簧的伸长量为5cm,∠cO′a=120°,重力加速度g取10m/s2,求:
如图所示,A、B都是重物,A被绕过小滑轮P的细线悬挂,B放在粗糙的水平桌面上,滑轮P被一根斜短线系于天花板上的O点,O′是三根细线的结点,细线bO′水平拉着物体B,cO′沿竖直方向拉着弹簧.弹簧、细线、小滑轮的重力不计,细线与滑轮之间的摩擦力可忽略,整个装置处于静止状态.若重物A的质量为2kg,弹簧的伸长量为5cm,∠cO′a=120°,重力加速度g取10m/s2,求: