题目内容
15.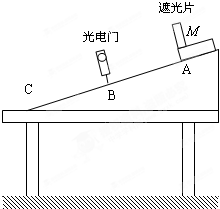 现要通过如图所示的实验装置验证机械能守恒定律:水平桌面上固定一斜面,斜面上的A点处放有一带长方形遮光片的滑块,滑块和遮光片的总质量为M,遮光片较窄且宽度为b,两条长边与导轨垂直.已知将滑块从A点由静止释放,遮光片经过斜面上的B处的光电门时间为t(t极小),A到斜面底端C的距离为d,A与C的高度差为h,当地的重力加速度为g.
现要通过如图所示的实验装置验证机械能守恒定律:水平桌面上固定一斜面,斜面上的A点处放有一带长方形遮光片的滑块,滑块和遮光片的总质量为M,遮光片较窄且宽度为b,两条长边与导轨垂直.已知将滑块从A点由静止释放,遮光片经过斜面上的B处的光电门时间为t(t极小),A到斜面底端C的距离为d,A与C的高度差为h,当地的重力加速度为g.①滑块经过B处时的速度大小为$\frac{b}{t}$;
②将滑块从A点由静止释放,若要验证A到B的过程中滑块及遮光片整体的机械能是否守恒,还需要测量一个物理量,这个物理量是AB之间的距离L,用测得量和已知量表示验证机械能守恒的关系式是MgL$\frac{h}{d}$=$\frac{1}{2}M$$\frac{b^2}{t^2}$.
分析 根据极短时间内的平均速度等于瞬时速度求出滑块经过B点的速度大小.抓住重力势能的减小量等于动能的增加量得出验证的表达式,从而确定还需测量的物理量.
解答 解:①根据极短时间内的平均速度等于瞬时速度知,滑块经过B点的速度为:$v=\frac{b}{t}$.
②重力势能的减小量为:△Ep=MgL$\frac{h}{d}$,动能的增加量为:$△{E}_{k}=\frac{1}{2}M{v}^{2}$=$\frac{1}{2}M$$\frac{b^2}{t^2}$.则验证的表达式为:MgL$\frac{h}{d}$=$\frac{1}{2}M$$\frac{b^2}{t^2}$.
可知还需测量的物理量为AB之间的距离L.
故答案为:①$\frac{b}{t}$,②AB之间的距离L,MgL$\frac{h}{d}$=$\frac{1}{2}M$$\frac{b^2}{t^2}$.
点评 解决本题的关键知道实验的原理,抓住动能的增加量等于重力势能的减小量得出机械能守恒的表达式是关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
5. 如图甲所示为电场中的一条电场线,在电场线上建立坐标轴,则坐标轴上O~x2间各点的电势分布如图乙所示,下列说法中正确的是( )
如图甲所示为电场中的一条电场线,在电场线上建立坐标轴,则坐标轴上O~x2间各点的电势分布如图乙所示,下列说法中正确的是( )
 如图甲所示为电场中的一条电场线,在电场线上建立坐标轴,则坐标轴上O~x2间各点的电势分布如图乙所示,下列说法中正确的是( )
如图甲所示为电场中的一条电场线,在电场线上建立坐标轴,则坐标轴上O~x2间各点的电势分布如图乙所示,下列说法中正确的是( )| A. | x1点的电场强度最小 | |
| B. | 0-x2之间,x轴附近的电场线分布先变密后变疏 | |
| C. | 一正电电荷从O点由静止释放,若仅受电场力作用,点电荷的加速度先增大后减小 | |
| D. | 一正电电荷从O点由静止释放,若仅受电场力作用,速度先增大后减小 |
6.取一小段通电直导线,其长为5cm,电流为5A,将它置于磁场中的P位置,所受安培力为1N,则P位置的磁感应强度为( )
| A. | B=4T | B. | B≤4T | C. | B≥4T | D. | 无法确定 |
7.在磁场中某一点,已经测出一段0.5cm长的导线中通入0.01A电流时,受到的安培力为5.0×10-6 N,则下列说法正确的是( )
| A. | 该点磁感应强度大小一定是0.1 T | |
| B. | 该点磁感应强度大小一定不大于0.1 T | |
| C. | 该点磁感应强度大小一定不小于0.1 T | |
| D. | 该点磁感应强度的方向即为导线所受磁场力的方向 |
5.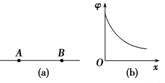 如图(a)所示,AB是某电场中的一条电场线,若有一电子以某一初速度且仅在电场力的作用下,沿AB由点A运动到点B,所经位置的电势随距A点的距离变化的规律如图(b)所示.以下说法正确的是( )
如图(a)所示,AB是某电场中的一条电场线,若有一电子以某一初速度且仅在电场力的作用下,沿AB由点A运动到点B,所经位置的电势随距A点的距离变化的规律如图(b)所示.以下说法正确的是( )
 如图(a)所示,AB是某电场中的一条电场线,若有一电子以某一初速度且仅在电场力的作用下,沿AB由点A运动到点B,所经位置的电势随距A点的距离变化的规律如图(b)所示.以下说法正确的是( )
如图(a)所示,AB是某电场中的一条电场线,若有一电子以某一初速度且仅在电场力的作用下,沿AB由点A运动到点B,所经位置的电势随距A点的距离变化的规律如图(b)所示.以下说法正确的是( )| A. | A、B两点的电场强度EA>EB | B. | A、B两点的电势φA<φB | ||
| C. | 电子在A、B两点的电势能EpA>EpB | D. | 电子在A、B两点的速度vA<vB |