题目内容
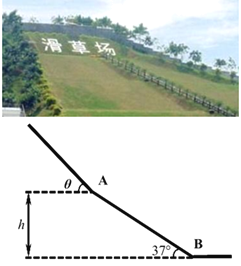
【题目】如图所示为一滑草场.某条滑道由上下两段滑道组成,下段滑道与水平面夹角为 α=37°,
高度为 h=12m,上段滑道与水平面夹角 θ 大于下段滑道.载人滑草车从上段滑道某处由静止开始自由下滑,经过 t1=4s 进入下段滑道,最后恰好静止于滑道的底端 B 点.已知上段滑道的加速度 为下段滑道加速度的 2.5 倍.滑草车在两段滑道上的运动均可视为匀变速直线运动,滑草车在两段滑道交接处 A点的速度大小不变.求:
(1)载人滑草车在上段滑道上滑行的距离;
(2)载人滑草车的最大速度及滑行的总时间;
(3)若改变下滑的起始位置,滑到底端的速度大小为 2m/s,求载人滑草车在上段滑道上滑行的距离.
【答案】(1)8m(2)14s(3)10m
【解析】
(1)设两段的长度分别是x1和x2,则:
![]()
设到达A的速度为v,第一段运动:
v2=2a1x1
第二段运动:
v2=2a2x2
由于上段滑道的加速度为下段滑道加速度的2.5倍,则:
![]()
(2)第一段运动为初速度等于0的匀加速直线运动,则:
![]()
可得:
a1=1m/s2
到达A的速度:
v=a1t1=1×4m/s=4m/s
第二段的加速度:
![]()
所以:
![]()
运动的总时间:
t=t1+t2=4s+10s=14s
(3)若滑到底端的速度大小为2m/s,到达A的速度为vm,则第二段滑道:
![]()
第一段滑道:
vm2=2ax1′
代入数据可得:
x′=10m

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目