题目内容
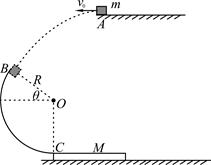
(15分)如图所示,两带有等量异种电荷的平行金属板M、N竖直放置,两板间的距离d=0.4m,现将一质量m=1.0×10-2kg、电荷量q=+4×10-5C的带电小球从两极板上方A点,以v0=2m/s的初速度水平抛出,A点距离两板上端的高度h=0.2m,之后小球恰从M板顶端位置无碰擦地进入板间,做直线运动,直至打在N板上的B点,设空气阻力不计,g=10m/s2,匀强电场只存在于M、N之间,求: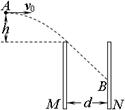
⑴小球进入电场时的速度大小和方向;
⑵两极板间的电势差U;
⑶小球到达B点时的动能。
⑴v= m/s,方向与水平方向成45°角斜向下;⑵U=1000V;⑶EkB=0.12J
m/s,方向与水平方向成45°角斜向下;⑵U=1000V;⑶EkB=0.12J
解析试题分析:⑴小球开始时做平抛运动,设小球进入电场时的速度大小为v,方向与水平方向间的夹角为θ,根据动能定理有:mgh= -
-
解得:v= =
= m/s=
m/s= m/s
m/s
根据几何关系有:cosθ=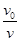 =
= ,即θ=45°
,即θ=45°
⑵由于小球进入电场后做直线运动,因此所受合力方向与速度方向共线,即所受电场力方向只能水平指向N板,所以有: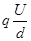 =mgtanθ
=mgtanθ
解得两极板间的电势差为:U= =1000V
=1000V
⑶对全程,根据动能定理有:mg(h+dtanθ)+qU=EkB-
解得:EkB=mg(h+dtanθ)+qU+ =0.12J
=0.12J
考点:本题主要考查了平抛运动规律、动能定理的应用,以及电场力的功的计算问题,属于中档题。

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
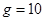 m/s2)
m/s2)
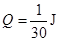 ,试求此过程中外力F对甲做的功.
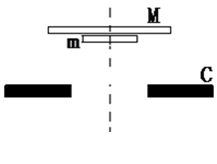
,试求此过程中外力F对甲做的功.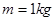 ,半径分别为
,半径分别为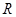 和
和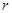 ,两板之间用一根长
,两板之间用一根长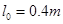 的轻绳将薄板中心相连结(未画出).开始时,两板水平放置并叠合在一起,静止于距离固定支架C高度
的轻绳将薄板中心相连结(未画出).开始时,两板水平放置并叠合在一起,静止于距离固定支架C高度 处. 然后自由下落到C上,支架上有一半径为
处. 然后自由下落到C上,支架上有一半径为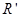 (
(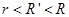 )的圆孔,圆孔与两薄板中心均在圆板中心轴线上. 薄板M与支架发生没有机械能损失的碰撞(碰撞时间极短). 碰撞后,两板即分离,直到轻绳绷紧.在轻绳绷紧的瞬间,两板立即具有共同速度.不计空气阻力,
)的圆孔,圆孔与两薄板中心均在圆板中心轴线上. 薄板M与支架发生没有机械能损失的碰撞(碰撞时间极短). 碰撞后,两板即分离,直到轻绳绷紧.在轻绳绷紧的瞬间,两板立即具有共同速度.不计空气阻力,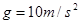 ,求:
,求: