ЬтФПФкШн
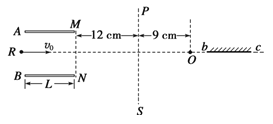
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкзјБъЯЕЕФЕквЛЁЂЫФЯѓЯоДцдквЛПэЖШЮЊ aЁЂДЙжБжНУцЯђЭтЕФгаНчдШЧПДХГЁЃЌДХИагІЧПЖШЕФДѓаЁЮЊ BЃЛдкЕкШ§ЯѓЯоДцдкгы y жсе§ЗНЯђГЩ ІШ=60ЁуНЧЕФдШЧПЕчГЁЁЃвЛИіСЃзгдДФмЪЭЗХжЪСПЮЊmЁЂЕчКЩСПЮЊ+qЕФСЃзгЃЌСЃзгЕФГѕЫйЖШПЩвдКіТдЁЃСЃзгдДдкЕу![]() ЪБЗЂГіЕФСЃзгЧЁКУДЙжБДХГЁБпНч EF ЩфГіЃЛНЋСЃзгдДбижБЯп PO вЦЖЏЕН Q ЕуЪБЃЌЫљЗЂГіЕФСЃзгЧЁКУВЛФмДг EF ЩфГіЁЃВЛМЦСЃзгЕФжиСІМАСЃзгМфЯрЛЅзїгУСІЁЃЧѓЃК
ЪБЗЂГіЕФСЃзгЧЁКУДЙжБДХГЁБпНч EF ЩфГіЃЛНЋСЃзгдДбижБЯп PO вЦЖЏЕН Q ЕуЪБЃЌЫљЗЂГіЕФСЃзгЧЁКУВЛФмДг EF ЩфГіЁЃВЛМЦСЃзгЕФжиСІМАСЃзгМфЯрЛЅзїгУСІЁЃЧѓЃК
ЃЈ1ЃЉдШЧПЕчГЁЕФЕчГЁЧПЖШ
ЃЈ2ЃЉPQ ЕФГЄЖШ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉ
ЃЈ2ЃЉ![]()
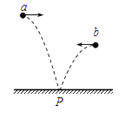
ЁОНтЮіЁПЃЈ1ЃЉСЃзгдДдкPЕуЪБЃЌСЃзгдкЕчГЁжаБЛМгЫйЃЌгЩЖЏФмЖЈРэ
![]()
НтЕУ![]()
СЃзгдкДХГЁжазідШЫйдВжмдЫЖЏЃЌИљОнХЃЖйЕкЖўЖЈТЩга![]()
гЩМИКЮЙиЯЕЕУ![]()
НтЕУ![]()
ЃЈ2ЃЉСЃзгдДдкQЕуЪБЃЌЩшOQ=dЃЌИљОнЖЏФмЖЈРэ![]()
ИљОнХЃЖйЕкЖўЖЈТЩга![]()
СЃзгдкДХГЁжадЫЖЏЕФЙьМЃгыБпНчEFЯрЧаЃЌгЩМИКЮЙиЯЕжЊ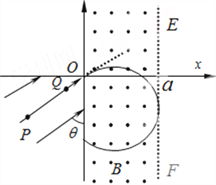
![]() ЙЪ
ЙЪ![]()
СЊСЂЕУ![]()
ГЄЖШ![]()

 дФЖСПьГЕЯЕСаД№АИ
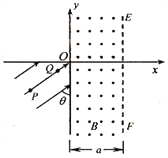
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁПФГЭЌбЇЮЊСЫЬНОПИЫзЊЖЏЪБЕФЖЏФмБэДяЪНЃЌЩшМЦСЫвЛЪЕбщЃКжЪСПЮЊmЕФОљдШГЄжБИЫвЛЖЫЙЬЖЈдкЙтЛЌзЊжсOДІЃЌИЫгЩЫЎЦНЮЛжУОВжЙЪЭЗХЃЌгУЙтЕчУХВтГіСэвЛЖЫAОЙ§ФГЮЛжУЪБЕФЫВЪБЫйЖШvAЃЌВЂМЧЯТИУЮЛжУгызЊжсOЕФИпЖШВюh.
(1)ЕїНкhЕФДѓаЁВЂМЧТМЖдгІЕФЫйЖШvAЃЌЪ§ОнШчЯТБэЃЎЮЊСЫаЮЯѓжБЙлЕиЗДгГvAКЭhЕФЙиЯЕЃЌгІбЁдё________(бЁЬюЁАvAЁБЁАv![]() ЁБЛђЁАvЁБ)ЮЊзнзјБъЃЌВЂдкзјБъжНжаБъУїзнзјБъЃЌЛГіЭМЯѓЃЎ
ЁБЛђЁАvЁБ)ЮЊзнзјБъЃЌВЂдкзјБъжНжаБъУїзнзјБъЃЌЛГіЭМЯѓЃЎ
зщДЮ | 1 | 2 | 3 | 4 | 5 | 6 |
h/m | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 |
vA(mЁЄsЃ1) | 1.23 | 1.73 | 2.12 | 2.46 | 2.74 | 3.00 |
v | 0.81 | 0.58 | 0.47 | 0.41 | 0.36 | 0.33 |
v (m2ЁЄsЃ2) | 1.50 | 3.00 | 4.50 | 6.05 | 7.51 | 9.00 |
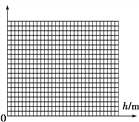
(2)ЕБЕижиСІМгЫйЖШgШЁ10 m/s2ЃЌНсКЯЭМЯѓЗжЮіЃЌИЫзЊЖЏЪБЕФЖЏФмEkЃН________(ЧыгУжЪСПmЁЂЫйЖШvAБэЪО)ЃЎ