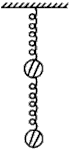题目内容
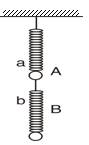
 如图,a、b两弹簧劲度系数均为K,两球质量均为m,不计弹簧的质量,两球静止,则两弹簧伸长量之和为________.
如图,a、b两弹簧劲度系数均为K,两球质量均为m,不计弹簧的质量,两球静止,则两弹簧伸长量之和为________.
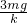
分析:a弹簧L1受到的弹力大小等于2G,b弹簧L2受到的弹力大小等于G,根据胡克定律分别求出两根弹簧伸长的长度,再求出静止时两弹簧伸长量之和.
解答:B球受到弹力大小为G,故b弹簧伸长量为xb=
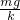 ,而A球弹力为2G,故a弹簧伸长量为xa=
,而A球弹力为2G,故a弹簧伸长量为xa=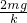 ;
;总伸长量为△x=xa+xb=
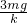 ;
;故答案为:
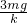 .
.点评:对于弹簧问题,关键分析弹簧的状态和弹力大小.

练习册系列答案
 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
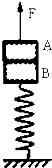 如图,A、B两个木块叠放在竖直轻弹簧上,mA=2kg,mB=1kg,轻弹簧的劲度系数为100N/m.在A上作用一个竖直向上的力F,使木块A由静止开始以2m/s2的加速竖直向上作匀加速运动,直到A、B分离时,弹簧的弹性势能减小了3.78J,g取10m/s2,则在这一匀加速运动的过程中有( )
如图,A、B两个木块叠放在竖直轻弹簧上,mA=2kg,mB=1kg,轻弹簧的劲度系数为100N/m.在A上作用一个竖直向上的力F,使木块A由静止开始以2m/s2的加速竖直向上作匀加速运动,直到A、B分离时,弹簧的弹性势能减小了3.78J,g取10m/s2,则在这一匀加速运动的过程中有( )| A、力F的最大值是24N | ||||
B、维持的时间是
| ||||
| C、A对B的压力做的功是-1.62J | ||||
| D、力F对木块做的功是2.7J |
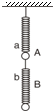 如图,a、b两弹簧劲度系数均为K,两球质量均为m,不计弹簧的质量,两球静止,则两弹簧伸长量之和为
如图,a、b两弹簧劲度系数均为K,两球质量均为m,不计弹簧的质量,两球静止,则两弹簧伸长量之和为