题目内容
12. 某同学利用数码相机连拍功能记录运动会上女子跳水比赛中运动员在10m跳台跳水的全过程.所拍摄的第一张照片恰为她们起跳的瞬间,第五张如图甲,该同学认为这时她们处在最高点,第二十一张如图乙,她们正好身体竖直、双手刚刚触及水面,查阅资料得知相机拍摄两张照片间隔时间T=0.1s(忽略相机曝光时间),设起跳时重心离台面及触水时重心离水面的距离相等,由以上材料:(g=10m/s2)
某同学利用数码相机连拍功能记录运动会上女子跳水比赛中运动员在10m跳台跳水的全过程.所拍摄的第一张照片恰为她们起跳的瞬间,第五张如图甲,该同学认为这时她们处在最高点,第二十一张如图乙,她们正好身体竖直、双手刚刚触及水面,查阅资料得知相机拍摄两张照片间隔时间T=0.1s(忽略相机曝光时间),设起跳时重心离台面及触水时重心离水面的距离相等,由以上材料:(g=10m/s2)(1)求运动员的起跳速度大小;
(2)分析第五张照片是在最高点吗?如果不是,此时运动员的重心是处于上升阶段还是下降阶段?
分析 (1)根据匀变速直线运动的位移时间公式求出运动员起跳时的速度大小.
(2)根据速度时间公式求出运动的时间,分析重心是处于上升阶段还是下降阶段.
解答 解:(1)运动员竖直上抛的时间为:
t=20T=20×0.1s=2s
根据x=${v}_{0}t-\frac{1}{2}g{t}^{2}$代入数据有:-10=$2{v}_{0}-\frac{1}{2}×10×4$,
解得:v0=5m/s
由v0=gt′得:$t′=\frac{{v}_{0}}{g}=\frac{5}{10}s=0.5s$,
因为0.5s>0.4s,所以第五张照片不是在最高点,运动员的重心处于上升阶段.
答:(1)运动员的起跳速度大小为5m/s;
(2)第五张照片不是在最高点,运动员的重心处于上升阶段.
点评 本题考查了竖直上抛运动的基本运用,知道竖直上抛运动的加速度不变,结合匀变速直线运动的位移公式和速度公式进行求解,难度不大.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
7.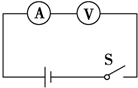 用两只完全相同的电流表分别改装成一只电流表和一只电压表.将它们串联起来接入电路中,如图所示,此时( )
用两只完全相同的电流表分别改装成一只电流表和一只电压表.将它们串联起来接入电路中,如图所示,此时( )
 用两只完全相同的电流表分别改装成一只电流表和一只电压表.将它们串联起来接入电路中,如图所示,此时( )
用两只完全相同的电流表分别改装成一只电流表和一只电压表.将它们串联起来接入电路中,如图所示,此时( )| A. | 两只电表的指针偏转角相同 | |
| B. | 两只电表的指针偏转角不确定 | |
| C. | 电流表指针的偏转角小于电压表指针的偏转角 | |
| D. | 电流表指针的偏转角大于电压表指针的偏转角 |
8.根据欧姆定律,下列说法中正确的是( )
| A. | 从关系式R=$\frac{U}{I}$可知,对于一个确定的导体来说,如果通过的电流越大,则导体两端的电压也越大 | |
| B. | 从关系式R=$\frac{U}{I}$可知,导体的电阻跟导体两端的电压成正比,跟导体中的电流成正比 | |
| C. | 从关系式R=$\frac{U}{I}$可知,导体中的电流跟导体两端的电压成正比,跟导体的电阻成反比 | |
| D. | 从关系式R=$\frac{U}{I}$可知,对于一个确定的导体来说,所加在的电压跟通过的电流的比值是一确定值 |
5.某品牌电动汽车在某次测试过程中数据如下表所示,请根据表中数据回答问题.
已知汽车在水平公路上沿直线行驶时所受阻力f跟行驶速率v和汽车所受重力mg的乘积成正比,即f=kmgv,其中k=2.0×10-3s/m.取重力加速度g=10m/s2.
(1)若汽车加速过程是匀加速直线运动,求这次测试中汽车的加速度大小a;
(2)求该电动汽车在平直公路上以额定功率行驶的最大速度以及以该速度行驶s=180km的距离时所消耗电能的费用(假设1kW•h电能的售价为0.50元).
| 整车行驶质量 | 1500kg |
| 额定功率 | 75kW |
| 加速过程 | 车辆从静止加速到30m/s所需时间为10s |
(1)若汽车加速过程是匀加速直线运动,求这次测试中汽车的加速度大小a;
(2)求该电动汽车在平直公路上以额定功率行驶的最大速度以及以该速度行驶s=180km的距离时所消耗电能的费用(假设1kW•h电能的售价为0.50元).
7.木星是太阳系中最大的行星,它有众多卫星.天文学家可以通过对木星的卫星以下哪几个量的研究,就可以精确地测算出木星的质量( )
| A. | 卫星的质量 | B. | 卫星的公转周期 | ||
| C. | 卫星的自转周期 | D. | 卫星绕木星的线速度 |
17.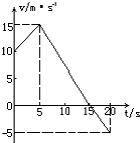 质量为1kg的物体做直线运动,其速度图象如图所示,则在前10s和后10s内,物体所受合外力的冲量分别是( )
质量为1kg的物体做直线运动,其速度图象如图所示,则在前10s和后10s内,物体所受合外力的冲量分别是( )
 质量为1kg的物体做直线运动,其速度图象如图所示,则在前10s和后10s内,物体所受合外力的冲量分别是( )
质量为1kg的物体做直线运动,其速度图象如图所示,则在前10s和后10s内,物体所受合外力的冲量分别是( )| A. | 2.5N•s,12.5N•s | B. | -2.5N•s,-12.5N•s | ||
| C. | 0,12.5N•s | D. | 0,-12.5N•s |
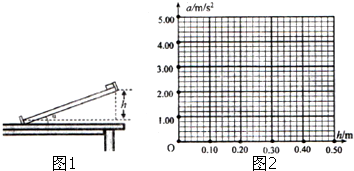
2.某研究性学习小组欲探究光滑斜面上物体下滑的加速度与物体质量及斜面倾角的关系.因为一般的长木板摩擦较大,学习小组决定用气垫导轨代替长木板,对气垫导轨进行改造,做成斜面,这样摩擦可以忽略不计,装置模型简化如图1所示,实验室提供器材如下:
A.气垫导轨(已知长度L);
B.质量为M的滑块(内部是空的,可放砝码,可视为质点);
C.质量为m的砝码若干个;
D.各种薄厚不等的方木块多个(垫气垫导轨备用);
E.米尺;
F.秒表.
实验过程:
第一步,保持斜面倾角不变,探究加速度与质量的关系.
(1)实验中,通过向滑块内放入砝码来改变滑块质量,只要测出滑块由斜面顶端滑至底端所用时间t,就可以由下面表达式$\frac{2L}{{t}^{2}}$求出滑块的加速度.
(2)某同学记录的实验数据如表所示,根据这些信息,判断以下结论正确的是BD.
A.在实验误差范围内,滑块的质量改变之后,其加速度改变较大
B.经过分析得出滑块的加速度和滑块的总质量没有关系
C.经过分析得出滑块的平均速度和滑块的总质量成正比
D.在实验误差范围内,滑块的质量改变之后,其下滑时间不改变
第二步,保持物体质量不变,探究加速度与倾角的关系.
实验中通过改变方木块垫放位置来调整气垫导轨的倾角.由于没有量角器,因此通过测量气垫导轨顶端到水平面高度h,求出倾角α的正弦值sinα=h/L.某同学记录了高度h和加速度a的对应值如下表:
(3)请根据上表中所给的数据,在图2坐标纸上通过描点绘出a-h图象.
(4)根据所绘出的图线,求出当地的重力加速度g=9.82m/s2.(保留三位有效数字)
A.气垫导轨(已知长度L);
B.质量为M的滑块(内部是空的,可放砝码,可视为质点);
C.质量为m的砝码若干个;
D.各种薄厚不等的方木块多个(垫气垫导轨备用);
E.米尺;
F.秒表.
实验过程:
第一步,保持斜面倾角不变,探究加速度与质量的关系.
(1)实验中,通过向滑块内放入砝码来改变滑块质量,只要测出滑块由斜面顶端滑至底端所用时间t,就可以由下面表达式$\frac{2L}{{t}^{2}}$求出滑块的加速度.
(2)某同学记录的实验数据如表所示,根据这些信息,判断以下结论正确的是BD.
| 时间t/s 质量 次数 | M | M+m | M+2m |
| 1 | 1.42 | 1.41 | 1.42 |
| 2 | 1.40 | 1.42 | 1.39 |
| 3 | 1.41 | 1.38 | 1.42 |
B.经过分析得出滑块的加速度和滑块的总质量没有关系
C.经过分析得出滑块的平均速度和滑块的总质量成正比
D.在实验误差范围内,滑块的质量改变之后,其下滑时间不改变
第二步,保持物体质量不变,探究加速度与倾角的关系.
实验中通过改变方木块垫放位置来调整气垫导轨的倾角.由于没有量角器,因此通过测量气垫导轨顶端到水平面高度h,求出倾角α的正弦值sinα=h/L.某同学记录了高度h和加速度a的对应值如下表:
| L (m) | 1.00 | ||||
| h (m) | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 |
| a (m/s2) | 0.970 | 1.950 | 2.925 | 3.910 | 4.880 |
(4)根据所绘出的图线,求出当地的重力加速度g=9.82m/s2.(保留三位有效数字)

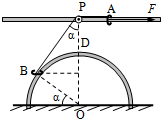 如图所示,用两根金属丝弯成一光滑半圆形轨道,竖直固定在地面上,其圆心为O、半径为0.3m.轨道正上方离地0.4m处固定一水平长直光滑杆,杆与轨道在同一竖直平面内,杆上P点处固定一定滑轮,P点位于O点正上方.A、B是质量均为2kg的小环,A套在杆上,B套在轨道上,一条不可伸长的细绳绕过定滑轮连接两环.两环均可看作质点,且不计滑轮大小与质量.现在A环上施加一个大小为55N的水平向右恒力F,使B环从地面由静止沿轨道上升.(g取10m/s2),求:
如图所示,用两根金属丝弯成一光滑半圆形轨道,竖直固定在地面上,其圆心为O、半径为0.3m.轨道正上方离地0.4m处固定一水平长直光滑杆,杆与轨道在同一竖直平面内,杆上P点处固定一定滑轮,P点位于O点正上方.A、B是质量均为2kg的小环,A套在杆上,B套在轨道上,一条不可伸长的细绳绕过定滑轮连接两环.两环均可看作质点,且不计滑轮大小与质量.现在A环上施加一个大小为55N的水平向右恒力F,使B环从地面由静止沿轨道上升.(g取10m/s2),求: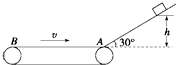 如图所示,倾角为30°的光滑斜面的下端有一水平传送带,传送带正以6m/s的速度运动,运动方向如图所示.一个质量为2kg的物体(物体可以视为质点),从h=3.2m高处由静止沿斜面下滑,物体经过A点时,不管是从斜面到传送带还是从传送带到斜面,都不计其动能损失.物体与传送带间的动摩擦因数为0.5,物体向左最多能滑到传送带左右两端AB的中点处,重力加速度g=10m/s2,求:
如图所示,倾角为30°的光滑斜面的下端有一水平传送带,传送带正以6m/s的速度运动,运动方向如图所示.一个质量为2kg的物体(物体可以视为质点),从h=3.2m高处由静止沿斜面下滑,物体经过A点时,不管是从斜面到传送带还是从传送带到斜面,都不计其动能损失.物体与传送带间的动摩擦因数为0.5,物体向左最多能滑到传送带左右两端AB的中点处,重力加速度g=10m/s2,求: