题目内容
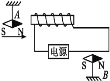
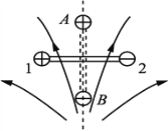
【题目】一根轻质杆长为2L,可绕固定于中点位置处的轴在竖直面内自由转动,杆两端固定有完全相同的小球1和小球2,它们的质量均为m,带电荷量分别为+q和–q,整个装置放在如图所示的关于竖直线对称的电场中。现将杆由水平位置静止释放,让小球1、2绕轴转动到竖直位置A、B两点,设A、B间电势差为![]() ,该过程中( )
,该过程中( )
A. 小球2受到电场力变小
B. 小球1电势能减少量小于![]()
C. 小球1、2的机械能总和增加量小于![]()
D. 小球1、2的动能总和增加了![]()
【答案】BD
【解析】
由图可知,杆由水平位置转到竖直位置时,球2所处的位置电场线变得密集,场强变大,则球2所受的电场力变大,选项A错误;根据电场线分布的对称性可知:开始时两个小球处于同一等势面上,转动后,小球1所在位置A的电势较低,小球2所在位置B的电势较高,根据等势面线电场线的关系知道,A、1间电势差小于2、B间的电势差,小球2的电势升高量大于小球1电势降低量,所以小球1的电势能减小量小于![]() qu,小球2的电势能减小量大于
qu,小球2的电势能减小量大于![]() qu,选项B正确;根据动能定理,系统的重力势能未变,则动能增加量等于电场力对系统做功,大小为uq,机械能增加量等于动能的增加量,即系统的机械能增加量也为uq,故C错误,D正确。故选BD。
qu,选项B正确;根据动能定理,系统的重力势能未变,则动能增加量等于电场力对系统做功,大小为uq,机械能增加量等于动能的增加量,即系统的机械能增加量也为uq,故C错误,D正确。故选BD。

练习册系列答案
相关题目