题目内容
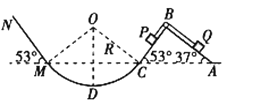
【题目】如图所示,半径![]() 的光滑圆弧面
的光滑圆弧面![]() 分别与光滑斜面体
分别与光滑斜面体![]() 和斜面
和斜面![]() 相切于
相切于![]() 、
、![]() 点,
点, ![]() 为圆弧圆心,
为圆弧圆心, ![]() 为圆弧最低点,斜面体
为圆弧最低点,斜面体![]() 固定在地面上,顶端
固定在地面上,顶端![]() 安装一定滑轮,一轻质软细绳跨过定滑轮(不计滑轮摩擦)分别连接小物块
安装一定滑轮,一轻质软细绳跨过定滑轮(不计滑轮摩擦)分别连接小物块![]() 、
、![]() (两边细绳分别与对应斜面平行),
(两边细绳分别与对应斜面平行), ![]() 、
、![]() 两物块保持静止,若
两物块保持静止,若![]() 、
、![]() 间距为
间距为![]() ,斜面MN粗糙且足够长,物块
,斜面MN粗糙且足够长,物块![]() 的质量
的质量![]() ,与
,与![]() 间的动摩擦因数
间的动摩擦因数![]() ,
,![]() ,取
,取![]() 。
。
(1).求小物块![]() 的质量
的质量![]() ;
;
(2).烧断细绳后,小物块![]() 第一次过
第一次过![]() 点后经
点后经![]() 到达
到达![]() 点(未画出),求
点(未画出),求![]() 、
、![]() 的间距
的间距![]() ;
;
(3).求小物块![]() 在
在![]() 斜面上滑行的总路程
斜面上滑行的总路程![]() 。
。
【答案】(1)4kg (2)0.17m (3)1m
【解析】
根据共点力平衡条件列式求解;先根据运动学公式求出M点速度,再根据牛顿第二定律求MN段上升和下降的加速度,再结合运动学公式求MK间距;直接根据动能定理全程列式求解。
(1)设细绳拉力大小为![]() ,对小物块
,对小物块![]() ,根据共点力平衡得
,根据共点力平衡得![]() ;对小物块
;对小物块![]() ,根据共点力平衡得
,根据共点力平衡得![]()
解得:![]()
(2)烧断细绳后,小物块![]() 沿
沿![]() 下滑的加速度
下滑的加速度![]() ,小物块
,小物块![]() 到达
到达![]() 点的速度
点的速度![]() ,根据机械能守恒定律知,小物块
,根据机械能守恒定律知,小物块![]() 在
在![]() 点的速度
点的速度![]() ,小物块
,小物块![]() 沿
沿![]() 上滑的加速度大小
上滑的加速度大小![]() ,小物块
,小物块![]() 沿
沿![]() 上滑的时间
上滑的时间![]() ,所以小物块
,所以小物块![]() 沿
沿![]() 上升到最高返回,小物块
上升到最高返回,小物块![]() 沿
沿![]() 下滑的加速度大小
下滑的加速度大小![]() ,则
,则![]() 、
、![]() 的间距
的间距![]() 。
。
(3)小物块最终在![]() 、
、![]() 间来回滑动,对全过程运用动能定理得
间来回滑动,对全过程运用动能定理得![]()
解得:![]()

练习册系列答案
相关题目