题目内容
【题目】如图所示,在竖直平面内有轨道ABC,其中AB段为水平直轨道,与质量m=0.5 kg的小物块(可视为质点)之间的动摩擦因数![]() =0.2,BC段为光滑半圆形轨道,轨道半径R=2m,轨道AB与BC在B点相切。小物块在水平拉力F=3N的作用下从A点由静止开始做匀加速直线运动,到达圆弧轨道的最低点B时撤去拉力,此时速度vB=10m/s。取g=10m/s2,则:
=0.2,BC段为光滑半圆形轨道,轨道半径R=2m,轨道AB与BC在B点相切。小物块在水平拉力F=3N的作用下从A点由静止开始做匀加速直线运动,到达圆弧轨道的最低点B时撤去拉力,此时速度vB=10m/s。取g=10m/s2,则:
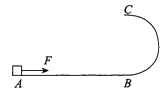
(1)拉力F做了多少功;
(2)经过B点后瞬间,物块对轨道的压力是多大;
(3)若物块从最高点C飞出后落到水平轨道上的D点(图中未画出),求BD间的距离。
【答案】(1)37.5J;(2)30N;(3)4m。
【解析】
试题分析:(1)由牛顿运动定律F-μmg=ma,解得a=4m/s2;
sAB=![]() =12.5m/s2,W=FsAB=37.5J
=12.5m/s2,W=FsAB=37.5J
(2)由牛顿第二定律N-mg=![]() ,解得N=30N;
,解得N=30N;
由牛顿第三定律得N′=N=30N;
(3)由机械能守恒定律2mgR+![]() mvc2=
mvc2=![]() mvB2;
mvB2;
由平抛规律得2R=![]() gt2,故x=vct,代入数据解得x=4m。
gt2,故x=vct,代入数据解得x=4m。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目