题目内容
14.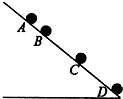 从斜面上某一位置每隔0.1s释放一些相同的小球,在连续释放几个小球之后,对斜面上运动的小球摄下照片如图所示,测得AB=15cm,BC=20cm.试求:
从斜面上某一位置每隔0.1s释放一些相同的小球,在连续释放几个小球之后,对斜面上运动的小球摄下照片如图所示,测得AB=15cm,BC=20cm.试求:(1)小球运动的加速度;
(2)拍摄时B球的速度;
(3)D、C两球间的距离;
(4)A球上面正在运动着的小球共有多少个?
分析 (1)分析题意,由△s=aT2可求得加速度;
(2)由平均速度等于中间时刻的瞬时速度可求得B球的速度;
(3)根据△s=aT2可求得两段时间内改变的位移,从而求得DC间的距离;
(4)由位移差值为常数可明确上方的小球数.
解答 解:因为任一小球从斜面下滑过程中加速度相同,所以同一时刻不同小球的位置分布与同一小球相隔0.1s时间在不同时刻位置分布完全相同.sAB、sBC、sCD都可以看成同一小球在0.1s时间内的位移.由于小球做匀变速直线运动,由△s=aT2,
所以(1)$a=\frac{{{s_{BC}}-{s_{AB}}}}{T^2}=\frac{(0.2-0.15)}{{{{0.1}^2}}}=5.0m/{s^2}$.
(2)由一段时间中点时刻速度等于这段时间的平均速度${v_B}=\frac{{{s_{BC}}+{s_{AB}}}}{2T}=\frac{(0.2+0.15)}{2×0.1}=1.75m/s$.
(3)因为△s=aT2=常量,
sCD-sBC=sBC-sAB,
故sCD=2sBC-sAB=2×0.2-0.15=0.25m
(4)△s=sBC-sAB=20-15=5cm.
因此,在A球上方,还有距A球分别为10cm和5cm的两个小球在运动.
答:(1)小球运动的加速度为5.0m/s2;
(2)拍摄时B球的速度为1.75m/s;
(3)D、C两球间的距离0.25m;
(4)A球上面正在运动着的小球共有2个.
点评 本题考查匀变速直线运动中规律的应用,要注意正确掌握△s=aT2,的应用的优点并在解题中多加练习.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.一群处于基态的氢原子吸收某种单色光子后,向外辐射了ν1、ν2、ν3三种频率的光子,且ν3>ν2>ν1,则( )
| A. | 被氢原子吸收的光子能量为hν3 | B. | 被氢原子吸收的光子能量为hν2 | ||
| C. | 被氢原子吸收的光子能量为hν1 | D. | 被氢原子吸收的光子能量为h(ν1+ν2) |
19. 如图所示,一重为8N的球固定在AB杆的上端,今用测力计斜向上拉球,使杆发生弯曲,此时测力计的示数为6N,则AB杆对球作用力大小可能为( )
如图所示,一重为8N的球固定在AB杆的上端,今用测力计斜向上拉球,使杆发生弯曲,此时测力计的示数为6N,则AB杆对球作用力大小可能为( )
 如图所示,一重为8N的球固定在AB杆的上端,今用测力计斜向上拉球,使杆发生弯曲,此时测力计的示数为6N,则AB杆对球作用力大小可能为( )
如图所示,一重为8N的球固定在AB杆的上端,今用测力计斜向上拉球,使杆发生弯曲,此时测力计的示数为6N,则AB杆对球作用力大小可能为( )| A. | 1 N | B. | 6 N | C. | 10 N | D. | 15 N |
3.在物理学发展的过程中,许多物理学家的科学研究推动了人类文明的进程.在对以下几位物理学家所作科学贡献的叙述中,正确的说法是( )
| A. | 亚里士多德认为两个从同一高度自由落下的物体,重物体与轻物体下落一样快 | |
| B. | 胡克认为只有在一定的条件下,弹簧的弹力才与弹簧的形变量成正比 | |
| C. | 牛顿应用“理想斜面实验”推翻了亚里士多德的“力是维持物体运动的原因”观点 | |
| D. | 英国物理学家卡文迪许用实验的方法测出万有引力常量G |
19.在“用单摆测重力加速度”的实验中,若测的g值比当地的标准值偏小,可能因为( )
| A. | 测摆长时摆线拉的过紧 | |
| B. | 测摆长时用摆线长代替摆长而漏加小球半径 | |
| C. | 测量周期时,将n次全振动误记成n+1次全振动 | |
| D. | 开始记时时,小球通过平衡位置时秒表按下的时刻滞后于小球通过平衡位置的时刻 |

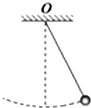 如图所示,质量为1kg的小球用细绳悬挂于O点,将小球拉离竖直位置释放后,到达最低点时的速度为2m/s,已知球心到悬点的距离为1m,重力加速度g=10m/s2,求小球在最低点时对绳的拉力的大小.
如图所示,质量为1kg的小球用细绳悬挂于O点,将小球拉离竖直位置释放后,到达最低点时的速度为2m/s,已知球心到悬点的距离为1m,重力加速度g=10m/s2,求小球在最低点时对绳的拉力的大小.