Question

【题目】如图，光滑的倾斜轨道BCD与光滑圆弧轨道DEFG相切于D点，轨道的倾角θ=37°，圆弧轨道的半径为R．一根轻弹簧沿轨道一端固定在B点，在另一端放置一质量为m的物块A，A与弹簧接触但不连接。现将A压缩至C点，CD之间的距离为R，静止释放，发现物块A恰好沿圆弧轨道通过最高点G．重力加速度为g。（取sin37°=，cos37°=）

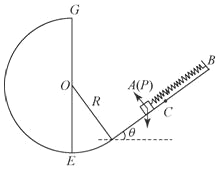
（1）求物块A运动至D点的速度大小vD。

（2）将A另换做物块P，将P同样压缩至C点静止释放，若要使P滑上圆弧轨道之后始终不脱离轨道，并能沿轨道原路返回，求P的质量mP与A的质量m的又会应满足的条件。

Answer 1

【答案】（1）（2）

【解析】

（1）物块A恰好沿圆弧轨道通过最高点G时，由重力提供向心力，根据牛顿第二定律得

mg=m

从D到G的过程，根据机械能守恒定律得：mgR（1+cosθ）+=

联立解得 vD=

（2）物块A从C到G的过程，由机械能守恒定律得：

Ep=+mg（R+Rcosθ﹣Rsinθ）

要使P滑上圆弧轨道之后始终不脱离轨道，并能沿轨道原路返回，P最高只能运动到与圆心O点等高处，物块P从C运动到圆心O等高处的过程，由机械能守恒定律得：

Ep=mpg（R﹣Rsinθ）

结合mg=m，解得 mP=