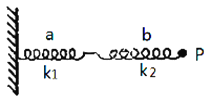Question

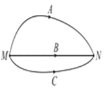
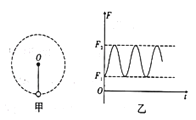
【题目】若宇航员到达某一星球后，做了如下实验:(1)让小球从距离地面高h处由静止开始下落，测得小球下落到地面所需时间为t;(2)将该小球用轻质细绳固定在传感器上的O点，如图甲所示。给小球一个初速度后，小球在竖直平面内绕O点做完整的圆周运动，传感器显示出绳子拉力大小随时间变化的图象所示(图中F1、F2为已知)。已知该星球近地卫星的周期为T，万有引力常量为G，该星球可视为均质球体。下列说法正确的是

A. 该星球的平均密度为B. 小球质量为

C. 该星球半径为D. 环绕该星球表面运行的卫星的速率为

Answer 1

【答案】ABD

【解析】

A.对近地卫星有，星球密度，体积，解得，故A正确。

B.小球通过最低点时拉力最大，此时有

最高点拉力最小，此时有

最高点到最低点，据动能定理可得

可得，小球做自由落体运动时，有

可得，，故B正确。

C.根据 及 可得：星球平均密度可表示为

可得，故C错误。

D.环绕该星球表面运行的卫星的速率可表示为

故D正确。