题目内容
7. 如图所示,半径R=1.0m的光滑圆弧轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与水平方向间的夹角θ=37°,另一端点C为轨道的最低点.C点右侧的光滑水平面上紧挨C点静止 放置一木板,木板质量M=1kg,上表面与C点等高.质量为m=1kg的物块(可视为质点)从空中A点以v0=1.2m/s的速度水平抛出,恰好从轨道的B端沿切线方向进入轨道.已知物块与木板间的动摩擦因数μ=0.2,取g=10m/s2.求:
如图所示,半径R=1.0m的光滑圆弧轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与水平方向间的夹角θ=37°,另一端点C为轨道的最低点.C点右侧的光滑水平面上紧挨C点静止 放置一木板,木板质量M=1kg,上表面与C点等高.质量为m=1kg的物块(可视为质点)从空中A点以v0=1.2m/s的速度水平抛出,恰好从轨道的B端沿切线方向进入轨道.已知物块与木板间的动摩擦因数μ=0.2,取g=10m/s2.求:(1)物块经过B点时的速度vB大小;
(2)物块经过C点时的动能Ek
(3)若木板足够长,物块在木板上相对滑动过程中产生的热量Q.
分析 (1)根据平抛运动的规律得出物体在B点的速度;
(2)对B到C段运用动能定理,求出物块经过C点的速度.
(3)物块在木板上滑动时,做匀减速运动,木板做匀加速直线运动,当速度相同后一起做匀速运动,结合牛顿第二定律和运动学公式求出共同运动的速度,根据能量守恒求出物块在木板上相对滑动过程中产生的热量Q
解答 解:(1)设物体在B点的速度为vB,在C点的速度为vC,从A到B物体做平抛运动,有:vBsinθ=v0
则 vB=$\frac{{v}_{0}}{sinθ}$=$\frac{1.2}{sin37°}$=2m/s
(2)从B到C,根据动能定理有:mgR(1+sinθ)=$\frac{1}{2}$$m{v}_{C}^{2}$-$\frac{1}{2}m{v}_{B}^{2}$
解得:vC=6m/s
动能为 EkC=$\frac{1}{2}m{v}_{C}^{2}$=18J
(3)物块在木板上相对滑动过程中由于摩擦力作用,最终将一起共同运动.设相对滑动时物体加速度为a1,木板加速度为a2,经过时间t达到共同运动速度为v,
则根据牛顿第二定律得:
μmg=ma1…
μmg=Ma2
由速度公式有 v=vC-a1t,v=a2t
根据能量守恒定律有:$\frac{1}{2}$(m+M)v2+Q=$\frac{1}{2}m{v}_{C}^{2}$
联立以上五式解得得:Q=9J
答:(1)物块经过B点时的速度vB大小是2m/s
(2)物块经过C点时的动能为18J;
(3)物块在木板上相对滑动过程中产生的热量Q为9J
点评 本题考查了动能定理、能量守恒的综合运用,对于第二问,也可以通过动量守恒求出共同的速度,也可以根据牛顿第二定律和运动学公式求出相对运动的位移大小,结合摩擦力与相对位移的乘积等于产生热量求出热量的大小.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案| A. | 法拉第发现了电磁感应现象,使人类迈进了使用电的时代 | |
| B. | 20世纪初,爱因斯坦建立了狭义相对论,得出了一些不同于经典力学的观念和结论 | |
| C. | 欧姆用实验研究了电流的热效应,总结出欧姆定律 | |
| D. | 19世纪中叶,焦耳和楞次先后各自独立发现了电流通过导体时产生热效应的规律,称为焦耳-楞次定律 |
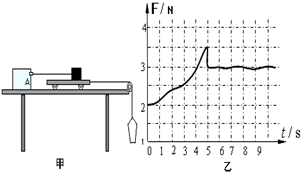 在探究摩擦力变化规律的实验中,特设计了如甲图所示的演示装置,力传感器A与计算机连接,可获得力随时间变化的规律,将力传感器固定在光滑水平桌面上,测力端通过细绳与一滑块相连(调节传感器高度可使细绳水平),滑块放在较长的小车上,小车一端连接一根轻绳并跨过光滑的轻定滑轮系一只空沙桶(调节滑轮可使桌面上部细绳水平),整个装置处于静止状态.实验开始时打开传感器同时缓慢向沙桶里倒入沙子,小车一旦运动起来,立即停止倒沙子,若力传感器采集的图象如乙图所示,则结合该图象,下列说法中正确的是( )
在探究摩擦力变化规律的实验中,特设计了如甲图所示的演示装置,力传感器A与计算机连接,可获得力随时间变化的规律,将力传感器固定在光滑水平桌面上,测力端通过细绳与一滑块相连(调节传感器高度可使细绳水平),滑块放在较长的小车上,小车一端连接一根轻绳并跨过光滑的轻定滑轮系一只空沙桶(调节滑轮可使桌面上部细绳水平),整个装置处于静止状态.实验开始时打开传感器同时缓慢向沙桶里倒入沙子,小车一旦运动起来,立即停止倒沙子,若力传感器采集的图象如乙图所示,则结合该图象,下列说法中正确的是( )| A. | 可求出空沙桶的重力 | |
| B. | 可求出滑块与小车之间的滑动摩擦力的大小 | |
| C. | 可求出滑块与小车之间的最大静摩擦力的大小 | |
| D. | 可判断第5秒后小车做匀速直线运动(滑块仍在车上) |
 如图所示一带负电的小球P的质量为m=4×10-4Kg,电量的大小为q=2.5×10-8C.用一条绝缘细线悬挂在电场中的O点,静止时,悬线偏离竖直方向θ=30°角.求所加的最小场强的大小及方向.
如图所示一带负电的小球P的质量为m=4×10-4Kg,电量的大小为q=2.5×10-8C.用一条绝缘细线悬挂在电场中的O点,静止时,悬线偏离竖直方向θ=30°角.求所加的最小场强的大小及方向.