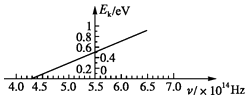
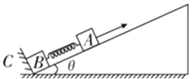
��Ŀ����
����Ŀ�������Ϊ���Ĺ⻬б�������������ᵯ�����ӵ����A��B�����ǵ������ֱ�Ϊ3m��2m�����ɵľ���ϵ��Ϊk��CΪһ�̶����壬ϵͳ���ھ�ֹ״̬������һ��б�淽��ĺ���F�����Aʹ֮��б�������˶�����B���뿪Cʱ��A���ٶ�Ϊv�����ٶȷ�����б�����ϡ���СΪa����
A. ��A���ٶȴﵽ���ʱ��B�ļ��ٶȴ�СΪ![]()
B. B���뿪Cʱ��������A�����Ĺ���Ϊ![]()
C. �Ӿ�ֹ��B���뿪C�Ĺ����У�A������λ��Ϊ![]()
D. �Ӿ�ֹ��B���뿪C�Ĺ����У�������A���Ĺ�Ϊ![]()
���𰸡�AC
����������ʼA���ھ�ֹ״̬�����ɴ���ѹ��������ƽ���У�3mgsin��=kx1����õ��ɵ�ѹ����Ϊ x1=![]() ����B���뿪Cʱ��B�Ե���ĵ���Ϊ�㣬�У�kx2=2mgsin������õ��ɵ��쳤��Ϊ x2=
����B���뿪Cʱ��B�Ե���ĵ���Ϊ�㣬�У�kx2=2mgsin������õ��ɵ��쳤��Ϊ x2=![]() ����֪�Ӿ�ֹ��B���뿪C�Ĺ����У�A������λ��x=x1+x2=
����֪�Ӿ�ֹ��B���뿪C�Ĺ����У�A������λ��x=x1+x2=![]() ����C��ȷ���Ӿ�ֹ��B���뿪C�Ĺ����У�������A���Ĺ� W=-3mgxsin��=-
����C��ȷ���Ӿ�ֹ��B���뿪C�Ĺ����У�������A���Ĺ� W=-3mgxsin��=-![]() ����D������ţ�ٵڶ����ɵã�F-3mgsin��-kx2=3ma�����F=5mgsin��+3ma���������A�����Ĺ���P=Fv=��5mgsin��+3ma��v����B����A���ٶȴﵽ���ʱ��A�ܵ��ĺ�����Ϊ0����F-3mgsin��-T��=0�����ԣ�T��=2mgsin��+3ma��B��б�淽���ܵ�������FB=T��-2mgsin��=2ma�������a��=
����D������ţ�ٵڶ����ɵã�F-3mgsin��-kx2=3ma�����F=5mgsin��+3ma���������A�����Ĺ���P=Fv=��5mgsin��+3ma��v����B����A���ٶȴﵽ���ʱ��A�ܵ��ĺ�����Ϊ0����F-3mgsin��-T��=0�����ԣ�T��=2mgsin��+3ma��B��б�淽���ܵ�������FB=T��-2mgsin��=2ma�������a��=![]() a����A��ȷ����ѡAC.
a����A��ȷ����ѡAC.