题目内容
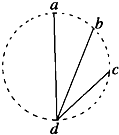
如图所示，ad、bd、cd是竖直面内三根固定的光滑细杆，a、b、c、d位于同一圆周上，a点为圆周的最高点，d点为最低点。每根杆上都套有一个小滑环（图中未画出），三个滑环分别从a、b、c处释放（初速为0），用t1、t2、t3依次表示各滑环到达d所用的时间，则（ ）
A．t1<t2<t3 B．t1>t2>t3
C．t3>t1>t2 D．t1=t2=t3
D
解析:
选任一杆上的环为研究对象，受力分析并建立坐标如图所示，设圆半径为R，由牛顿第二定律得，
①
再由几何关系，细杆长度
②
设下滑时间为
，则
③
由以上三式得，
可见下滑时间与细杆倾角无关，所以D正确。由此题我们可以得出一个结论。
结论：物体沿着位于同一竖直圆上的所有光滑弦由静止下滑，到达圆周最低点的时间相等。
推论：若将图1倒置成图2的形式，同样可以证明物体从最高点由静止开始沿不同的光滑细杆到圆周上各点所用的时间相等。
练习册系列答案
黄冈小状元解决问题天天练系列答案
相关题目
（2004?江西）如图所示，ad、bd、cd是竖直面内三根固定的光滑细杆，a、b、c、d位于同一圆周上，a点为圆周的最高点，d点为最低点．每根杆上都套着一个小滑环（图中未画出），三个滑环分别从a、b、c处释放（初速为0），用t1、t2、t3依次表示滑环到达d所用的时间，则（ ）
（2011?甘肃二模）如图所示，AD、BD、CD都是光滑的直角斜面，斜面固定在水平地面上，现使一小物体分别从A、B、C点由静止开始下滑到D点，所用时间分别为t1、t2、t3，则（ ）
如图所示，ad、bd、cd是竖直面内三根固定的光滑细杆，a、b、c、d位于同一圆周上，a点为圆周的最高点，d点为最低点．每根杆上都套着一个完全相同的小滑环（图中未画出），三个滑环分别从a、b、c点无初速释放，关于它们下滑过程的下列说法中正确的是（ ）
如图所示，ad、bd、cd是竖直面内三根固定的光滑细杆，a、b、c、d位于同一圆周，a点为圆周的最高点，d为圆周的最低点．每根杆上都套着一个质量相同的小滑环（图中未画出），三个滑环分别a、b、c处释放（初速度为零），关于它们下滑的过程，下列说法中正确的是（ ）| A、重力对它们的冲量相同 | B、弹力对它们的冲量相同 | C、合外力对它们的冲量相同 | D、它们的动能增量相同 |
如图所示，ad、bd、 cd是竖直面内的三根固定的光滑细杆，a、ｂ、c、ｄ位于同一圆周上，ａ点为圆周上最高点，ｄ点为圆周上最低点。每根杆上都套有一个小圆环，三个圆环分别从ａ、ｂ、c处由静止释放，用t1 、t2、t3依次表示各环到达d点所用的时间，则（ ）
| A．t 1＜t2＜ t3 | B．t 1＞t2＞ t3 |
| C．t 3＞t1＞ t2 | D．t 1＝t2＝t3 |